【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A( ![]() ,0),点B(0,3),点O(0,0)
,0),点B(0,3),点O(0,0)
(1)过边OB上的动点D(点D不与点B,O重合)作DE丄OB交AB于点E,沿着DE折叠该纸片,点B落在射线BO上的点F处.
①如图,当D为OB中点时,求E点的坐标;
②连接AF,当△AEF为直角三角形时,求E点坐标;
(2)P是AB边上的动点(点P不与点B重合),将△AOP沿OP所在的直线折叠,得到△A′OP,连接BA′,当BA′取得最小值时,求P点坐标(直接写出结果即可).
参考答案:
【答案】
(1)解:①∵DE⊥OB,OA⊥OB,
∴DE∥OA.
∵D为OB中点,
∴DE为△BOA的中位线,
∴点E为线段A、B的中点,
∴点E的坐标为( ![]() ,
, ![]() ).
).
②由折叠可知:△BDE≌△FDE,
∴∠EFB=∠ABO=30°,DF=BD,
∴∠AEF=∠ABO+∠BFE=60°≠90°.
∵△AEF是直角三角形,
∴∠AFE=90°或∠EAF=90°.
(i)当∠AFE=90°时,如图1所示.
∠AFO=180°﹣∠AFE﹣∠EFB=60°.
在Rt△AOF中,∠AFO=60°,AO= ![]() ,
,
∴∠FAO=30°,AF=2OF,
∵ ![]() =AO,
=AO,
∴OF=1,AF=2.
在Rt△DEF中,∠DFE=30°,DF=BD= ![]() =1,
=1,
∴EF=2DE,
∵ ![]() =DF=1,
=DF=1,
∴DE= ![]() ,DF=
,DF= ![]() .
.
∵OD=OF+DF=2.
∴点E的坐标为( ![]() ,2);
,2);
(ii)当∠EAF=90°时,如图2所示.
∵∠AOB=90°,∠ABO=30°,
∴∠BAO=60°,
∴∠FAO=∠EAF﹣∠BAO=30°.
在Rt△AOF中,∠FAO=30°,AO= ![]() ,
,
∴AF=2OF,
∵ ![]() =AO,
=AO,
∴OF=1,AF=2.
在Rt△DEF中,∠DFE=30°,DF= ![]() =2,
=2,
∴EF=2DE,
∵ ![]() =DF,
=DF,
∴DE= ![]() .
.
∵OD=DF﹣OF=1,
∴点E的坐标为( ![]() ,1).
,1).
综上所述:当△AEF为直角三角形时,E点坐标为( ![]() ,2)或(
,2)或( ![]() ,1)
,1)
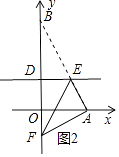
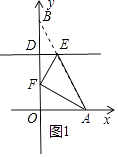
(2)解:由折叠可知:△AOP≌△A′OP,
∴OA′=OA= ![]() ,∠AOP=∠A′OP,
,∠AOP=∠A′OP,
又∵OB=3,
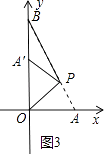
∴当点A′在y轴上时,BA′取最小值,如图3所示.
∵∠AOB=90°,
∴∠AOP=45°,
∴直线OP的解析式为y=x.
设直线AB的解析式为y=kx+b,
将A( ![]() ,0)、B(0,3)代入y=kx+b中,
,0)、B(0,3)代入y=kx+b中,
![]() ,解得:
,解得: ![]() ,
,
∴直线AB的解析式为y=﹣ ![]() x+3.
x+3.
联立直线OP、AB的解析式成方程组,
![]() ,解得:
,解得: 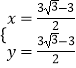 ,
,
∴当BA′取得最小值时,P点坐标为( ![]() ,
, ![]() ).
).
【解析】(1)①由D为OB中点结合DE∥OA,可得出DE为△BOA的中位线,再根据点A、B的坐标即可得出点E的坐标;②根据折叠的性质结合角的计算可得出∠AEF=60°≠90°,分∠AFE=90°和∠EAF=90°两种情况考虑,利用含30度角的直角三角形以及勾股定理即可求出点E的坐标;(2)根据三角形的三边关系,找出当点A′在y轴上时,BA′取最小值,根据折叠的性质可得出直线OP的解析式,再根据点A、B的坐标利用待定系数法求出直线AB的解析式,联立两直线解析式成方程组,解之即可得出点P的坐标.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形.仔细观察图形可知:
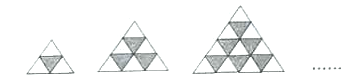
第1个图形中有1块黑色的瓷砖,可表示为
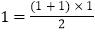 ;
;第2个图形中有3块黑色的瓷砖,可表示为
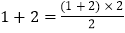 ;
;第3个图形中有6块黑色的瓷砖,可表示为
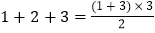 ;
;则第
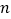 个图形中有__________块黑色的瓷砖(
个图形中有__________块黑色的瓷砖(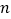 为正整数).
为正整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )

A.155° B.170° C.105° D.145°
-
科目: 来源: 题型:
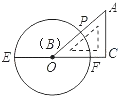
查看答案和解析>>【题目】如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x,则x的取值范围是( )
A.30≤x≤60
B.30≤x≤90
C.30≤x≤120
D.60≤x≤120 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大海中有两个岛屿A与B,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°,在点F处测得∠AFP=60°,∠BFQ=60°.
(1)判断AE,AB的数量关系,并说明理由;
(2)求∠BAE的度数.

-
科目: 来源: 题型:
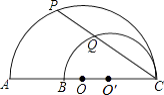
查看答案和解析>>【题目】如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=20cm,则PQ的值为( )
A.10cm
B.10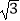 cm
cm
C.12cm
D.16cm -
科目: 来源: 题型:
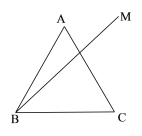
查看答案和解析>>【题目】如图,等边△ABC中,BM是ABC内部的一条射线,且
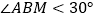 ,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.(1)依题意补全图形;
(2)若ABM ,求BDC 的大小(用含的式子表示);
(3)用等式表示线段PB,PC与PE之间的数量关系,并证明.
相关试题

