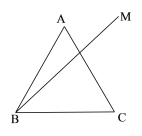
【题目】如图,等边△ABC中,BM是ABC内部的一条射线,且![]() ,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
(1)依题意补全图形;
(2)若ABM ,求BDC 的大小(用含的式子表示);
(3)用等式表示线段PB,PC与PE之间的数量关系,并证明.
参考答案:
【答案】(1)见解析;(2) 60°+![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)正确画图;
(2)根据对称得:BM是AD的垂直平分线,则BA=BD,根据等腰三角形的性质和等边三角形可得结论;
(3)在射线PD上截取PF使PF=PB,连接BF,如图,先证明△BPF是等边三角形,再证明△BFC≌△BPD,则CF=PD=2PE.根据线段的和可得结论.
(1)如图所示:
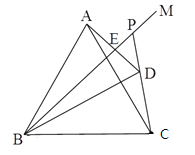
(2∵点A与点D关于BM对称,∴BM是AD的垂直平分线,∴BA=BD.
∵∠ABM=α,∴∠ABD=2∠ABM=2α.
∵等边△ABC,∴BA=CB=BD,∠ABC=60°,∴∠DBC=∠ABC-∠ABD =60°-![]() ,∴∠BDC=∠DCB=
,∴∠BDC=∠DCB=![]() (180°
(180°![]() ∠DBC)=60°+
∠DBC)=60°+![]() .
.
(3)结论:PB=PC+2PE.证明如下:
在射线PD上截取PF使PF=PB,连接BF.
∵BA=BD,∠ABD=![]() ,∴∠BDA=∠BAD=90°
,∴∠BDA=∠BAD=90°![]()
![]() .
.
∵∠BDC=60°+![]() ,∴∠PDE=180-(∠BDA+∠BDC)=30°.
,∴∠PDE=180-(∠BDA+∠BDC)=30°.
∵∠DEP=90°,∴PD=2PE.
∵∠BPF=∠DPE=90°![]() ∠PDE=60°,PF=PB,∴△BPF是等边三角形,∴∠BPF=∠BFP=60°.
∠PDE=60°,PF=PB,∴△BPF是等边三角形,∴∠BPF=∠BFP=60°.
∵∠BDC=∠DCB,∴∠BDP=∠BCF.
在△BFC和△BPD中,∵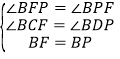 ,∴△BFC≌△BPD,∴CF=PD=2PE,∴PB= PC+BF=PC+2PE.
,∴△BFC≌△BPD,∴CF=PD=2PE,∴PB= PC+BF=PC+2PE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(
 ,0),点B(0,3),点O(0,0)
,0),点B(0,3),点O(0,0)
(1)过边OB上的动点D(点D不与点B,O重合)作DE丄OB交AB于点E,沿着DE折叠该纸片,点B落在射线BO上的点F处.
①如图,当D为OB中点时,求E点的坐标;
②连接AF,当△AEF为直角三角形时,求E点坐标;
(2)P是AB边上的动点(点P不与点B重合),将△AOP沿OP所在的直线折叠,得到△A′OP,连接BA′,当BA′取得最小值时,求P点坐标(直接写出结果即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大海中有两个岛屿A与B,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°,在点F处测得∠AFP=60°,∠BFQ=60°.
(1)判断AE,AB的数量关系,并说明理由;
(2)求∠BAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=20cm,则PQ的值为( )
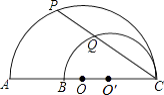
A.10cm
B.10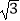 cm
cm
C.12cm
D.16cm -
科目: 来源: 题型:
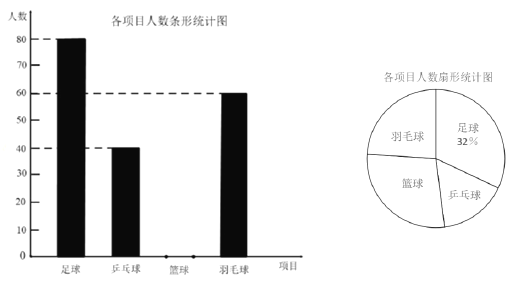
查看答案和解析>>【题目】某学校举行“每天锻炼一小时,健康生活一辈子”为主题的体育活动,并开展了以下体育项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项。为了解选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)求选择篮球项目的人数在扇形统计图中所占的百分比?
(4)若该学校有1500人,请你估计该学校选择乒乓球项目的学生人数约是多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E在BC边上,且AE⊥BC于点E,DE平分∠CDA.若BE∶EC=1∶2,则∠BCD的度数为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列每个图形及相应推出的结论,其中正确的是( )
A.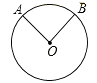
∵
∴∠AOB=80°
B.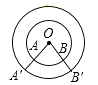
∵∠AOB=∠A′O′B′
∴
C.
∵
∴AB=CD
D.
∵MN垂直平分AD
∴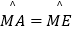
相关试题

