【题目】正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上.
①若AB=BE,求∠DAE度数;
②求证:CE=EF;
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.

参考答案:
【答案】(1)①22.5°;②证明见解析;(2)![]() 或
或![]() .
.
【解析】
(1)①先求得∠ABE的度数,然后依据等腰三角形的性质和三角形内角和定理求得∠BAE的度数,然后可求得∠DAE度数;
②先利用正方形的对称性可得到∠BAE=∠BCE,然后在证明又∠BAE=∠EFC,通过等量代换可得到∠BCE=∠EFC;
(2)当点F在BC上时,过点E作MN⊥BC,垂直为N,交AD于M.依据等腰三角形的性质可得到FN=CN,从而可得到NC的长,然后可得到MD的长,在Rt△MDE中可求得ED的长;当点F在CB的延长线上时,先根据题意画出图形,然后再证明EF=EC,然后再按照上述思路进行解答即可.
(1)①∵ABCD为正方形,∴∠ABE=45°,
又∵AB=BE,∴∠BAE![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠DAE=90°﹣67.5°=22.5°;
②∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,∴∠BAE=∠BCE,
又∵∠ABC=∠AEF=90°,∴∠BAE=∠EFC,∴∠BCE=∠EFC,∴CE=EF;
(2)如图1,过点E作MN⊥BC,垂直为N,交AD于M,
∵CE=EF,∴N是CF的中点,
∵BC=2BF,∴![]() ,
,
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴ED![]() DM
DM![]() CN
CN![]() ;
;
如图2,过点E作MN⊥BC,垂直为N,交AD于M,
∵正方形ABCD关于BD对称,∴△ABE≌△CBE,∴∠BAE=∠BCE,
又∵∠ABF=∠AEF=90°,∴∠BAE=∠EFC,
∴∠BCE=∠EFC,∴CE=EF,∴FN=CN,
又∵BC=2BF,∴FC=3,∴CN![]() ,∴EN=BN
,∴EN=BN![]() ,∴DE
,∴DE![]() ,
,

综上所述:ED的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】记面积为18cm2的平行四边形的一条边长为x(cm),这条边上的高线长为y(cm).
(1)写出y关于x的函数表达式及自变量x的取值范围;
(2)在如图直角坐标系中,用描点法画出所求函数图象;
(3)若平行四边形的一边长为4cm,一条对角线长为
 cm,请直接写出此平行四边形的周长.
cm,请直接写出此平行四边形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是半径为
是半径为  的⊙
的⊙  的直径,
的直径,  是圆上异于
是圆上异于  ,
,  的任意一点,
的任意一点,  的平分线交⊙
的平分线交⊙  于点
于点  ,连接
,连接  和
和  ,△
,△  的中位线所在的直线与⊙
的中位线所在的直线与⊙  相交于点
相交于点  、
、  ,则
,则 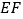 的长是.
的长是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的二次函数
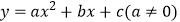 的图象中,观察得出了下面五条信息:
的图象中,观察得出了下面五条信息:
①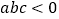 ;②
;② 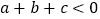 ;③
;③ 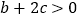 ;④
;④ 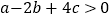 ;⑤
;⑤ 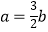 ,
,
你认为其中正确信息的个数有个.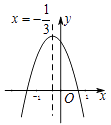
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
 是△
是△ 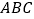 的外接圆,
的外接圆, 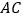 为直径,弦
为直径,弦 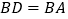 ,
, 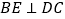 交
交 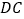 的延长线于点
的延长线于点 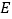 ,求证:
,求证: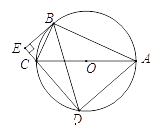
(Ⅰ)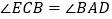 ;
;
(Ⅱ)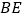 是⊙
是⊙ 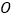 的切线.
的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:
 有一个角为
有一个角为 的等腰三角形是等边三角形;
的等腰三角形是等边三角形; 等腰直角三角形一定是轴对称图形;
等腰直角三角形一定是轴对称图形; 有一条直角边对应相等的两个直角三角形全等;
有一条直角边对应相等的两个直角三角形全等; 到线段两端距离相等的点在这条线段的垂直平分线上.
到线段两端距离相等的点在这条线段的垂直平分线上.正确的个数有

A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用长为
 的铝合金条制成“日”字形窗框,若窗框的宽为
的铝合金条制成“日”字形窗框,若窗框的宽为  ,窗户的透光面积为
,窗户的透光面积为  (铝合金条的宽度不计).
(铝合金条的宽度不计).
(Ⅰ)求出 与
与  的函数关系式;
的函数关系式;
(Ⅱ)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
相关试题

