【题目】如图,用长为 ![]() 的铝合金条制成“日”字形窗框,若窗框的宽为
的铝合金条制成“日”字形窗框,若窗框的宽为 ![]() ,窗户的透光面积为
,窗户的透光面积为 ![]() (铝合金条的宽度不计).
(铝合金条的宽度不计).
(Ⅰ)求出 ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
(Ⅱ)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
参考答案:
【答案】解:(Ⅰ)∵大长方形的周长为6m,宽为xm,
∴长为 ![]() m,
m,
∴y=x ![]() =﹣
=﹣ ![]() (0<x<2),
(0<x<2),
(Ⅱ)由(Ⅰ)可知:y和x是二次函数关系,
a=﹣ ![]() <0,
<0,
∴函数有最大值,
当x=﹣ ![]() =1时,y最大=
=1时,y最大= ![]() m2,
m2,
答:窗框的长和宽分别为1.5m和1m时才能使得窗户的透光面积最大,此时的最大面积为1.5 m.
【解析】(Ⅰ)根据周长可用x表示出其长,再由面积公式可得y与x的关系式;
(Ⅱ)由(Ⅰ)可得a<0,可求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上.
①若AB=BE,求∠DAE度数;
②求证:CE=EF;
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
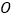 是△
是△ 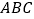 的外接圆,
的外接圆, 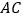 为直径,弦
为直径,弦 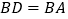 ,
, 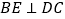 交
交 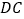 的延长线于点
的延长线于点 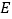 ,求证:
,求证: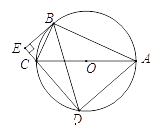
(Ⅰ)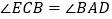 ;
;
(Ⅱ)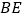 是⊙
是⊙ 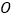 的切线.
的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:
 有一个角为
有一个角为 的等腰三角形是等边三角形;
的等腰三角形是等边三角形; 等腰直角三角形一定是轴对称图形;
等腰直角三角形一定是轴对称图形; 有一条直角边对应相等的两个直角三角形全等;
有一条直角边对应相等的两个直角三角形全等; 到线段两端距离相等的点在这条线段的垂直平分线上.
到线段两端距离相等的点在这条线段的垂直平分线上.正确的个数有

A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图
 所示放置,图
所示放置,图 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC, 请找出图
请找出图 中的全等三角形,并给予说明
中的全等三角形,并给予说明 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母 ;
; 试说明:
试说明: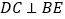 .
.
-
科目: 来源: 题型:
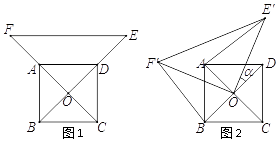
查看答案和解析>>【题目】如图1,已知
 为正方形
为正方形  的中心,分别延长
的中心,分别延长  到点
到点  ,
,  到点
到点  ,使
,使  ,
,  ,连结
,连结 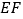 ,将△
,将△  绕点
绕点  逆时针旋转
逆时针旋转  角得到△
角得到△ 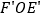 (如图2).连结
(如图2).连结  、
、  .
.
(Ⅰ)探究 与
与  的数量关系,并给予证明;
的数量关系,并给予证明;
(Ⅱ)当 ,
,  时,求:
时,求:
① 的度数;
的度数;
② 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 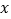 轴交于
轴交于  、
、  两点(点
两点(点  在点
在点  的左侧),点
的左侧),点  的坐标为
的坐标为  ,与
,与  轴交于点
轴交于点  ,作直线
,作直线  .动点
.动点  在
在 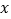 轴上运动,过点
轴上运动,过点  作
作  轴,交抛物线于点
轴,交抛物线于点  ,交直线
,交直线  于点
于点  ,设点
,设点  的横坐标为
的横坐标为 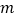 .
.
(Ⅰ)求抛物线的解析式和直线 的解析式;
的解析式;
(Ⅱ)当点 在线段
在线段  上运动时,求线段
上运动时,求线段  的最大值;
的最大值;
(Ⅲ)当以 、
、 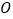 、
、  、
、  为顶点的四边形是平行四边形时,直接写出
为顶点的四边形是平行四边形时,直接写出 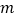 的值.
的值.
相关试题

