【题目】如图, ![]() 是半径为
是半径为 ![]() 的⊙
的⊙ ![]() 的直径,
的直径, ![]() 是圆上异于
是圆上异于 ![]() ,
, ![]() 的任意一点,
的任意一点, ![]() 的平分线交⊙
的平分线交⊙ ![]() 于点
于点 ![]() ,连接
,连接 ![]() 和
和 ![]() ,△
,△ ![]() 的中位线所在的直线与⊙
的中位线所在的直线与⊙ ![]() 相交于点
相交于点 ![]() 、
、 ![]() ,则
,则 ![]() 的长是.
的长是.
参考答案:
【答案】4 ![]()
【解析】如图所示:
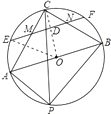
∵PC是∠APB的角平分线,∴∠APC=∠CPB,
![]()
![]() ∴AC=BC
∴AC=BC
∵AB是直径,
∴∠ACB=90.
即△ABC是等腰直角三角形,
连接OC,交EF于点D,则OC⊥AB;
∵MN是△ABC的中位线,
∴MN∥AB;
∴OC⊥EF,OD= ![]() OC=2.
OC=2.
连接OE,根据勾股定理,得:DE= ![]() =2
=2 ![]() ,
,
∴EF=2ED=4 ![]() .
.
故答案为:![]() .
.
连接OE、OC,交EF于点D.易证出△ABC是等腰直角三角形,则OC⊥AB;由MN是△ABC的中位线可知OC⊥EF,进而求出OD的长,再由勾股定理可求出DE的长,由垂径定理可得EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△
 和△
和△  都是等腰直角三角形,
都是等腰直角三角形,  ,
,  ,
,  ,
,  是
是  的中点.若将△
的中点.若将△  绕点
绕点  旋转一周,则线段
旋转一周,则线段  长度的取值范围是( )
长度的取值范围是( )
A.
B.
C.
D.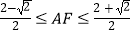
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】记面积为18cm2的平行四边形的一条边长为x(cm),这条边上的高线长为y(cm).
(1)写出y关于x的函数表达式及自变量x的取值范围;
(2)在如图直角坐标系中,用描点法画出所求函数图象;
(3)若平行四边形的一边长为4cm,一条对角线长为
 cm,请直接写出此平行四边形的周长.
cm,请直接写出此平行四边形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的二次函数
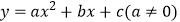 的图象中,观察得出了下面五条信息:
的图象中,观察得出了下面五条信息:
①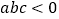 ;②
;② 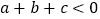 ;③
;③ 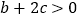 ;④
;④ 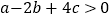 ;⑤
;⑤ 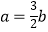 ,
,
你认为其中正确信息的个数有个.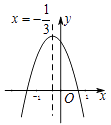
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上.
①若AB=BE,求∠DAE度数;
②求证:CE=EF;
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
 是△
是△ 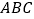 的外接圆,
的外接圆, 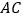 为直径,弦
为直径,弦 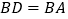 ,
, 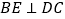 交
交 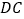 的延长线于点
的延长线于点 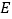 ,求证:
,求证: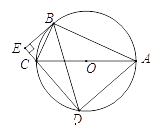
(Ⅰ)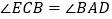 ;
;
(Ⅱ)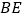 是⊙
是⊙ 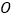 的切线.
的切线.
相关试题

