【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM= ![]() AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.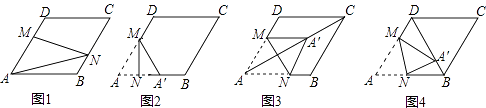
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)![]()
(2)1,解:②在菱形ABCD中,AC平分∠DAB,∵∠DAB=60°,∴∠DAC=∠CAB=30°,∵△AMN沿MN翻折得到△A′MN,∴AC⊥MN,AM=A′M,AN=A′N,;∴∠AMN=∠ANM=60°,∴AM=AN,∴AM=A′M=AN=A′N,∴四边形AM A′N是菱形;,③在菱形ABCD中,AB=AD,∴∠ADB=∠ABD=60°,∴∠BA′M=∠DMA′+∠ADB,∴A′M=AM=2,∠NA′M=∠A=60°,∴∠NA′B=∠DMA′,∴△DMA′∽△BA′N,∴ ![]() =
= ![]() ,∵MD=
,∵MD= ![]() AD=1,A′M=2,∴
AD=1,A′M=2,∴ ![]() =
= ![]()
【解析】解:(1)如图1,

过点N作NG⊥AB于G,
∵四边形ABCD是菱形,
∴AD∥BC,OD=OB,
∴ ![]() =
= ![]() =1,
=1,
∴BN=DM= ![]() AD=1,
AD=1,
∵∠DAB=60°,
∴∠NBG=60°
∴BG= ![]() ,GN=
,GN= ![]() ,
,
∴AN= ![]() =
= ![]() =
= ![]() ;
;
故答案为: ![]() ;
;
( 2 )①当点A′落在AB边上,则MN为AA′的中垂线,
∵∠DAB=60°AM=2,
∴AN= ![]() AM=1,
AM=1,
故答案为:1;
(1)过点N作NG⊥AB于G,构造直角三角形,根据菱形的性质得出AD∥BC,OD=OB,∠NBG=60° ,根据平行线分线段成比例定理得出DM∶BN=OD∶OB=1,从而得出BN=DM=1 ,利用含30°的直角三角形的边的关系得出BG、GN的长,利用勾股定理解决问题;
(2)①利用线段中垂线的性质得到MN⊥AA',利用含30°的直角三角形的边的关系得出AN的长;
②利用菱形的性质得到对角线平分每一组对角,得到∠DAC=∠CAB=30°,根据翻折的性质得到AC⊥MN,AM=A′M,AN=A′N,∠AMN=∠ANM=60°,AM=AN,AM=A′M=AN=A′N,四边形AM A′N是菱形
③根据菱形的性质得到AB=AD,∠ADB=∠ABD=60°,求得∠NA′M=∠DMA′+∠ADB,证得A′M=AM=2,∠NA′M=∠A=60°,得到∠NA′B=∠DMA′,从而判断出△DMA′∽△BA′N,利用相似三角形对应边成比例得到结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:ax2﹣4a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,代数式x2(2x)3﹣x(x+8x4)的值是( )
A.4
B.-4
C.0
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2x+7+3x﹣2,其中x=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中的真命题是
A. 同位角相等B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角D. 在同一平面内,如果a∥b,b∥c,则a∥c
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.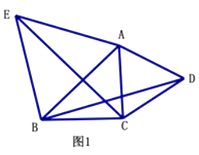
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.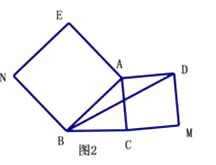
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
相关试题

