[题目]因式分解:ax2﹣4a= ．题目和参考答案 ——青夏教育精英家教网—

【题目】因式分解：ax2﹣4a= ．

参考答案：

【答案】a（x﹣2）（x+2）
【解析】解：ax2﹣4a
=a（x2﹣4）
=a（x﹣2）（x+2）．
所以答案是：a（x﹣2）（x+2）．

相关试题

科目： 来源： 题型：

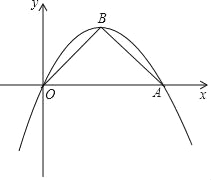
【题目】如图，在平面直角坐标系xOy，已知二次函数y=﹣x2+bx的图象过点A（4，0），顶点为B，连接AB、BO．
（1）求二次函数的表达式；
（2）若C是BO的中点，点Q在线段AB上，设点B关于直线CQ的对称点为B'，当△OCB'为等边三角形时，求BQ的长度；
（3）若点D在线段BO上，OD=2DB，点E、F在△OAB的边上，且满足△DOF与△DEF全等，求点E的坐标．
查看答案和解析>>
科目： 来源： 题型：

【题目】利用不等式的基本性质求下列不等式的解集,并说出变形的依据.
(1)若x+2 012>2 013,则x__________；(______________________________)
(2)若2x>-,则x__________；(______________________________)
(3)若-2x>-,则x__________；(______________________________)
(4)若->-1,则x__________.(______________________________)
查看答案和解析>>
科目： 来源： 题型：

【题目】指出下列各式成立的条件：
(1)由mx<n，得x<；
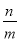(2)由a<b，得ma>mb；
(3)由a>－5，得a2≤－5a；
(4)由3x>4y，得3x－m>4y－m.
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，A（-5，0），B（-3，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB．∠CDA=90°．点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时时间t秒．

（1）求点C的坐标；
（2）当∠BCP=15°时，求t的值；
（3）以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值．
查看答案和解析>>
科目： 来源： 题型：

【题目】当x=2时，代数式x2（2x）3﹣x（x+8x4）的值是（　　）
A.4
B.-4
C.0
D.1
查看答案和解析>>
科目： 来源： 题型：

【题目】在图1﹣﹣图4中，菱形ABCD的边长为3，∠A=60°，点M是AD边上一点，且DM= AD，点N是折线AB﹣BC上的一个动点．

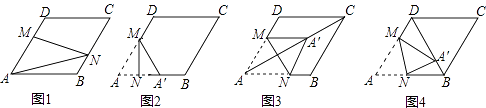
（1）如图1，当N在BC边上，且MN过对角线AC与BD的交点时，则线段AN的长度为．
（2）当点N在AB边上时，将△AMN沿MN翻折得到△A′MN，如图2，
①若点A′落在AB边上，则线段AN的长度为；
②当点A′落在对角线AC上时，如图3，求证：四边形AM A′N是菱形；
③当点A′落在对角线BD上时，如图4，求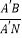的值．
查看答案和解析>>