搜索
【题目】下列命题中的真命题是
A. 同位角相等B. 在同一平面内，如果a⊥b，b⊥c，则a⊥c
C. 相等的角是对顶角D. 在同一平面内，如果a∥b，b∥c，则a∥c
参考答案：
【答案】D
【解析】
利用对顶角的性质，垂直的判定，平行线的判定以及同位角逐一分析得出答案即可．
A、两直线平行，同位角相等，本选项错误；
B、在同一平面内，如果a⊥b，b⊥c，则a∥c，本选项错误；
C、相等的角不一定是对顶角，本选项错误；
D、在同一平面内，如果a∥b，b∥c，则a∥c，本选项正确．
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】当x=2时，代数式x2（2x）3﹣x（x+8x4）的值是（ ）
A.4
B.-4
C.0
D.1 -
科目： 来源： 题型：
查看答案和解析>>【题目】在图1﹣﹣图4中，菱形ABCD的边长为3，∠A=60°，点M是AD边上一点，且DM=
AD，点N是折线AB﹣BC上的一个动点．
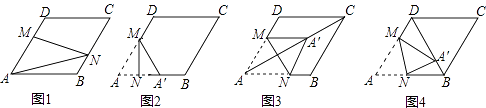
（1）如图1，当N在BC边上，且MN过对角线AC与BD的交点时，则线段AN的长度为 ．
（2）当点N在AB边上时，将△AMN沿MN翻折得到△A′MN，如图2，
①若点A′落在AB边上，则线段AN的长度为；
②当点A′落在对角线AC上时，如图3，求证：四边形AM A′N是菱形；
③当点A′落在对角线BD上时，如图4，求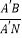
的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：2x+7+3x﹣2，其中x=2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据所学知识完成小题：
（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等边△ABE和等边△ACD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．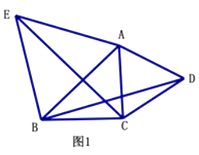
（2）【深入探究】如图2，△ABC中，∠ABC=45°，AB=5cm，BC=3cm，分别以AB、AC为边向外作正方形ABNE和正方形ACMD，连接BD，求BD的长．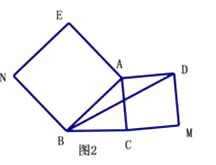
（3）如图3，在（2）的条件下，以AC为直角边在线段AC的左侧作等腰直角△ACD，求BD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为落实“垃圾分类”，环卫部门要求垃圾要按A，B，C三类分别装袋，投放，其中A类指废电池，过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料，废纸等可回收垃圾．甲投放了一袋垃圾，乙投放了两袋垃圾，这两袋垃圾不同类．
（1）直接写出甲投放的垃圾恰好是A类的概率；
（2）求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】列不等式：a的相反数的绝对值与3的和是正数．
相关试题
