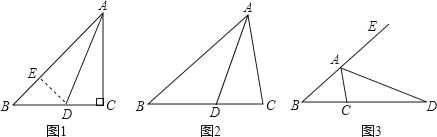
【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
参考答案:
【答案】(1)猜想:AB=AC+CD(2)猜想:AB+AC=CD.
【解析】试题分析:(1)首先在AB上截取AE=AC,连接DE,易证△ADE≌△ADC(SAS),则可得∠AED=∠C,ED=CD,又由∠AED=∠ACB,∠ACB=2∠B,所以∠AED=2∠B,即∠B=∠BDE,易证DE=CD,则可求得AB=AC+CD;
(2)首先在BA的延长线上截取AE=AC,连接ED,易证△EAD≌△CAD,可得ED=CD,∠AED=∠ACD,又由∠ACB=2∠B,易证DE=EB,则可求得AC+AB=CD.
试题解析:(1)猜想:AB=AC+CD.
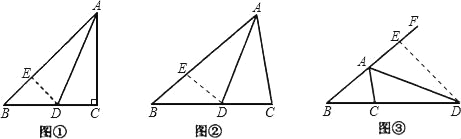
证明:如图②,在AB上截取AE=AC,连接DE,
∵AD为∠BAC的角平分线时,
∴∠BAD=∠CAD,
∵AD=AD,
∴△ADE≌△ADC(SAS),
∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴EB=ED,
∴EB=CD,
∴AB=AE+DE=AC+CD.
(2)猜想:AB+AC=CD.
证明:在BA的延长线上截取AE=AC,连接ED.
∵AD平分∠FAC,
∴∠EAD=∠CAD.
在△EAD与△CAD中,
AE=AC,∠EAD=∠CAD,AD=AD,
∴△EAD≌△CAD(SAS).
∴ED=CD,∠AED=∠ACD.
∴∠FED=∠ACB,
又∵∠ACB=2∠B
∴∠FED=2∠B,∠FED=∠B+∠EDB,
∴∠EDB=∠B,
∴EB=ED.
∴EA+AB=EB=ED=CD.
∴AC+AB=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用
 表示不大于
表示不大于 的最大整数,例如:
的最大整数,例如: ,
, ,
, ;用
;用 表示大于
表示大于 的最小整数,例如:
的最小整数,例如: ,
, ,
, .解决下列问题:
.解决下列问题:(1)
 = ,,
= ,, = ;
= ;(2)若
 =2,则
=2,则 的取值范围是 ;若
的取值范围是 ;若 =-1,则
=-1,则 的取值范围是 ;
的取值范围是 ;(3)已知
 ,
, 满足方程组
满足方程组 ,求
,求 ,
, 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在以
 为原点的平面直角坐标系中,有不在坐标轴上的两个点
为原点的平面直角坐标系中,有不在坐标轴上的两个点 、
、 ,设
,设 的坐标为
的坐标为 ,点
,点 的坐标
的坐标
(1)若
 与坐标轴平行,则
与坐标轴平行,则 ;
;(2)若
 、
、 、
、 满足
满足 和
和 ,
, 轴,垂足为
轴,垂足为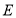 ,
,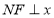 轴,垂足为
轴,垂足为 .
.①求四边形
 的面积;
的面积;②连
 、
、 、
、 ,若
,若 的面积大于
的面积大于 而不大于
而不大于 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是△ABC的角平分线,点E.F分别在边AB.BC上,且ED∥BC,EF∥AC,求证:
(1)BE等于CF
(2)∠ABC=60゜,∠ADB=100゜,求∠AEF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解我市市民2018年乘坐公交车的每人月均花费情况,相关部门随机调查了1000人的相关信息,并绘制了如图所示的频数直方图,根据图中提供的信息,有下列说法(每组值包括最低值,不包括最高值):①乘坐公交车的月均花费在60元~80元的人数最多;②月均花费在160元(含160元)以上的人数占所调查总人数的10%;③在所调查的1000人中,至少有一半以上的人的月均花费超过75元;④为了让市民享受更多的优惠,相关部门拟确定一个折扣标准,计划使30%左右的人获得优惠,那么可以是乘坐公交车的月均花费达到100元(含100元)以上的人享受折扣.

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2﹣
x2﹣ x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有 名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
相关试题

