【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设![]() ,
,![]() ,
,![]() ,请探索
,请探索![]() ,
,![]() ,
,![]() 满足的等量关系。
满足的等量关系。

参考答案:
【答案】(1)全等;证明见解析;(2)是,理由见解析;(3)c2=a2+ab+b2.
【解析】
试题分析:(1)由正三角形的性质得∠CAB=∠ABC=∠BCA=60°,AB=BC,证出∠ABD=∠BCE,由ASA证明△ABD≌△BCE即可;、
(2)由全等三角形的性质得出∠ADB=∠BEC=∠CFA,证出∠FDE=∠DEF=∠EFD,即可得出结论;
(3)作AG⊥BD于G,由正三角形的性质得出∠ADG=60°,在RtΔADG中,DG=![]() b,AG=
b,AG=![]() b, 在RtΔABG中,由勾股定理即可得出结论.
b, 在RtΔABG中,由勾股定理即可得出结论.
试题解析: (1)△ABD≌△BCE≌△CAF;理由如下:
∵△ABC是正三角形,
∴∠CAB=∠ABC=∠BCA=60°,AB=BC,
∵∠ABD=∠ABC﹣∠2,∠BCE=∠ACB﹣∠3,∠2=∠3,
∴∠ABD=∠BCE,
在△ABD和△BCE中,
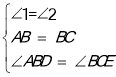 ,
,
∴△ABD≌△BCE(ASA);
(2)△DEF是正三角形;理由如下:
∵△ABD≌△BCE≌△CAF,
∴∠ADB=∠BEC=∠CFA,
∴∠FDE=∠DEF=∠EFD,
∴△DEF是正三角形;
(3)作AG⊥BD于G,如图所示:

∵△DEF是正三角形,
∴∠ADG=60°,
在Rt△ADG中,DG=![]() b,AG=
b,AG=![]() b,
b,
在Rt△ABG中,c2=(a+![]() b)2+(
b)2+(![]() b)2,
b)2,
∴c2=a2+ab+b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成ABABC共5个区,A区是边长为a m的正方形,C区是4个边长为b m的小正方形组成的正方形.

(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40 m,b=20 m,求整个长方形运动场的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112-4×2.11×2.22+2.222”,她觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=-1,y=1
x=1,y=0
x=3,y=2
x=2,y=-1
x=2,y=3
A=2x-y
-3
2
4
5
1
B=4x2-4xy+y2
9
4
16
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请利用A与B之间的关系计算:4×2.112-4×2.11×2.22+2.222.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(P点与A、B两点不重合).如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=-x2+1的勾股点的坐标.
(2)如图②,已知抛物线y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1,
 )是抛物线的勾股点,求抛物线的函数表达式.
)是抛物线的勾股点,求抛物线的函数表达式.(3)在(2)的条件下,点Q在抛物线上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(1,﹣4)是一次函数y=kx+b的图象和反比例函数y=
 的图象的两个交点.、(1)求△AOB的面积;(2)求不等式kx+b﹣
的图象的两个交点.、(1)求△AOB的面积;(2)求不等式kx+b﹣ <0的解集(请直接写出答案).
<0的解集(请直接写出答案).
-
科目: 来源: 题型:
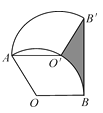
查看答案和解析>>【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点在x轴上,顶点B在y轴上,顶点C在函数
 (x>0)的图象上,且BC∥x轴.将△ABC沿y轴正方向平移,使点A的对应点
(x>0)的图象上,且BC∥x轴.将△ABC沿y轴正方向平移,使点A的对应点 落在此函数的图象上,则平移的距离为 .
落在此函数的图象上,则平移的距离为 .
相关试题

