搜索
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112－4×2.11×2.22＋2.222”，她觉得太麻烦，估计应该有可以简化计算的方法，就去请教崔老师．崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
（1）填写下表:
x＝－1，y＝1 | x＝1，y＝0 | x＝3，y＝2 | x＝2，y＝－1 | x＝2，y＝3 | |
A＝2x－y | －3 | 2 | 4 | 5 | 1 |
B＝4x2－4xy＋y2 | 9 | 4 | 16 |
（2）观察表格，你发现A与B有什么关系?
解决问题:
（3）请利用A与B之间的关系计算:4×2.112－4×2.11×2.22＋2.222．
参考答案：
【答案】（1）25 ，1 ；（2）A2＝B 即(2x－y)2＝4x2－4xy＋y2 ；（3）4
【解析】
（1）将x和y的值分别代入B＝4x2－4xy＋y2中求出B的值即可得出答案；
（2）根据（1）中补全的B的值，观察A和B的关系即可得出答案；
（3）根据（2）得到的公式将x=2.11，y=2.22代入即可得出答案.
解：（1）当x=2，y=-1时，B＝4x2－4xy＋y2=
=25，
当x=2，y=3时，B＝4x2－4xy＋y2=
=1；
（2）A2＝B 即(2x－y)2＝4x2－4xy＋y2
（3）原式＝(2×2.11－2.22)2
＝4
-
科目： 来源： 题型：
查看答案和解析>>【题目】有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的记录如下：
（1）这8筐白菜中，最接近25千克的那筐白菜为______千克；
（2）以每筐25千克为标准，这8筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2元，则出售这8筐白菜可卖多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（2015湖州）如图，已知抛物线C1：
和C2：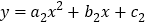
都经过原点，顶点分别为A，B，与x轴的另一交点分别为M，N，如果点A与点B，点M与点N都关于原点O成中心对称，则称抛物线C1和C2为姐妹抛物线，请你写出一对姐妹抛物线C1和C2，使四边形ANBM恰好是矩形，你所写的一对抛物线解析式是____________________和__________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一个长方形运动场被分隔成ABABC共5个区，A区是边长为a m的正方形，C区是4个边长为b m的小正方形组成的正方形．
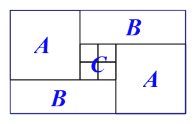
（1）列式表示每个B区长方形场地的周长，并将式子化简；
（2）列式表示整个长方形运动场的周长，并将式子化简；
（3）如果a＝40 m，b＝20 m，求整个长方形运动场的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在透明纸面上有一数轴(如图1)，折叠透明纸面．
（1）若表示1的点与表示－1的点重合，则表示－7的点与表示 的点重合；
（2）若表示－2的点与表示6的点重合，回答以下问题:
①表示12的点与表示 的点重合；
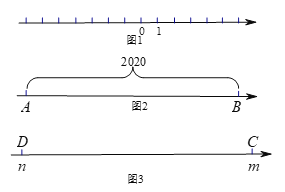
②如图2，若数轴上AB两点之间的距离为2020(点A在点B的左侧)，且AB两点经折叠后重合，则AB两点表示的数分别是 ．
（3）如图3，若m和n表示的点C和点D经折叠后重合(m＞n)，折痕与数轴的交点为折痕点．已知线段CD上两点P、Q (点P在点Q的左侧，PQ＜CD)，PQ＝a．当线段PQ的端点与折痕点重合时，求PQ两点表示的数分别是多少?(用含m，n，a的代数式表示)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】给出下列算式
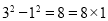
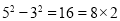
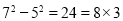
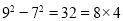
(1)观察上面一系列式子，猜想第五个式子？
(2)用含n的式子表示其规律(n为正整数)
(3)计算
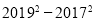的值，此时n是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】问题：探究一次函数y=kx+k+2（k是不为0常数）图象的共性特点，探究过程：小明尝试把x=-1代入时，发现可以消去k，竟然求出了y=2．老师问：结合一次函数图象，这说明了什么？小组讨论得出：无论k取何值，一次函数y=kx+k+2的图象一定经过定点（-1，2），老师：如果一次函数的图象是经过某一个定点的直线，那么我们把像这样的一次函数的图象定义为“点旋转直线”．已知一次函数y=（k+3）x+（k-1）的图象是“点旋转直线”
（1）一次函数y=（k+3）x+（k-1）的图象经过的定点P的坐标是__________．
（2）已知一次函数y=（k+3）x+（k-1）的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3，求k值；
②若△AOB的面积为1，求k值．
相关试题
