搜索
【题目】如图，在ABCD中，P1、P2是对角线BD的三等分点．求证：四边形APlCP2是平行四边形．
参考答案：
【答案】见解析
【解析】
由题意可得 BP1=DP2， AB=CD，AB//CD，根据平行线的性质可得∠ABP1=∠CDP2，证明△ABP1≌△CDP2，根据全等三角形的性质可得AP1=CP2，同理可证：CP1=AP2，根据两组对边分别相等的四边形是平行四边形即可得结论.
∵P1，P2是对角线BD的三等分点，ABCD是平行四边形，
∴BP1=DP2， AB=CD，AB//CD，
∴∠ABP1=∠CDP2，
在△ABP1和△CDP2中，
，
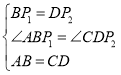∴△ABP1≌△CDP2(SAS)，
∴AP1=CP2，
同理可证：CP1=AP2，
∴四边形AP1CP2是平行四边形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把一块三角板放在直角坐标系第一象限内，其中30°角的顶点A落在y轴上，直角顶点C落在x轴的（
，0）处，∠ACO=60°，点D为AB边上中点，将△ABC沿x轴向右平移，当点A落在直线y=x﹣3上时，线段CD扫过的面积为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．
（1）如图①，当α=90°时，求AE′，BF′的长；
（2）如图②，当α=135°时，求证AE′=BF′，且AE′⊥BF′；
（3）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,若果∠1＝∠2，那么添加下列任何一个条件：（1）
，（2）
，（3）∠B＝∠D，（4）∠C＝∠AED， 其中能判定△ABC∽△ADE的个数为
A. 1 B. 2 C. 3 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB=60°，在AD上截取AE=AB，连接BE，EO，并求∠BEO的角度（要求：尺规作图，保留痕迹，不写作法）
-
科目： 来源： 题型：
查看答案和解析>>【题目】为推动阳光体育活动的广泛开展，引导学生积极参加体育锻炼，学校准备购买一批运动鞋供学生借用．现从各年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据图中提供的信息，解答下列问题：
（1）本次接受随机抽样调查的学生人数为 人，图①中的m的值为 ，图①中“38号”所在的扇形的圆心角度数为 ；
（2）本次调查获取的样本数据的众数是 ，中位数是 ；
（3）根据样本数据，若学校计划购买200双运动鞋，建议购买36号运动鞋多少双？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某水果生产基地，某天安排30名工人采摘枇杷或草莓（每名工人只能做其中一项工作），并且每人每天摘0.4吨枇杷或0.3吨草莓，当天的枇杷售价每吨2000元，草莓售价每吨3000元，设安排其中x名工人采摘枇杷，两种水果当天全部售出，销售总额达y元．
（1）求y与x之间的函数关系式；
（2）若要求当天采摘枇杷的数量不少于草莓的数量，求销售总额的最大值．
相关试题
