【题目】为了解全校学生上学的交通方式,我校九年级(21)班的5名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
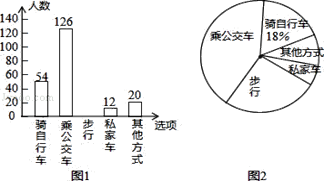
(1)本次接受调查的总人数是 人,其中“步行”的人数是 人;
(2)在扇形统计图中,“乘公交车”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
参考答案:
【答案】(1) 300,88;(2)42%,24°;(3)![]() .
.
【解析】试题分析:(1)用骑自行车的人数除以它所占的百分比即可得到调查的总人数,再用总人数-骑自行车的人数-乘公交车的人数-私家车的人数-其他方式的人数即可得到“步行”的人数;
(2)用“乘公交车”的人数÷总人数即可得到其所占的百分比,用“其他方式”的人数÷总人数再乘以360°得到“其他方式”所在扇形的圆心角度数;
(3)先画树状图展示所有20种等可能的结果数,再找出选出1名男生和1名女生的结果数,然后根据概率公式求解.
试题解析:解:(1)本次接受调查的总人数为54÷18%=300(人),“步行”的人数=300-54-126-12-20=88(人);
(2)“乘公交车”的人数所占的百分比是=![]() =42%;扇形统计图中“其他方式”所在扇形的圆心角度数为
=42%;扇形统计图中“其他方式”所在扇形的圆心角度数为![]() ×360°=24°;
×360°=24°;
(3)画树状图为:

共有20种等可能的结果数,其中选出1名男生和1名女生的结果数为12种,所以恰好选出1名男生和1名女生的概率=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当﹣2<x<2时,下列函数中,函数值y随自变量x增大而增大的有( )个.
①y=2x;②y=2﹣x;③y=﹣
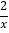 ;④y=x2+6x+8.
;④y=x2+6x+8.A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位长度后所得直线l′的函数解析式为_____.
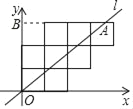
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有9张卡片,分别写有1到9这就个数字,将它们的背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,若数a使关于x的不等式组
 有解,且使函数
有解,且使函数 在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )
在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )A. 10 B. 11 C. 12 D. 13
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由几个边长为1个单位的正方体搭成的几何体.


(1)请画出这个几何体的三视图;
(2)这个几何体的体积为______个立方单位;
(3)若保持上述正方体搭成的几何体的俯视图不变,各位置的正方体个数可以改变(正方体的总数目不变),则搭成的几何体的表面积最大为_____个平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县某公司参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量
 (单位:个)与销售单价
(单位:个)与销售单价 (单位:元/个)之间的关系式为
(单位:元/个)之间的关系式为 .
.(1) 若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润
 (单位:元)与销售单价
(单位:元)与销售单价 (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;(2) 在(1)问的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
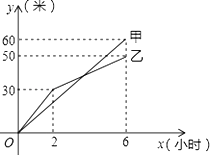
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

