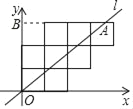
【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位长度后所得直线l′的函数解析式为_____.
参考答案:
【答案】![]()
【解析】
设直线l和八个正方形的最上面交点为A,过点A作AB⊥y轴于点B,过点A作AC⊥x轴于点C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标,再利用待定系数法可求出该直线l的解析式,再根据平移规律即可得到直线l′的函数解析式.
解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴![]()
∴AB![]() ,
,
∴OC![]() ,
,
由此可知直线l经过![]()
设直线l为y=kx,
则![]()
![]()
∴直线l解析式为![]()
∴直线l向右平移3个单位长度后所得直线l′的函数解析式为![]()
故答案为:![]()
-
科目: 来源: 题型:
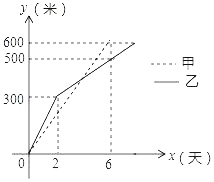
查看答案和解析>>【题目】甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(单位:米)与挖掘时间x(单位:天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③当x=4时,甲、乙两队所挖管道长度相同;④甲队比乙队提前2天完成任务.正确的是_____(直接填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图与探究:
如图,已知点A、O、B是正方形网格的格点(网格线的交点),点P是∠AOB的边0B上的一点.
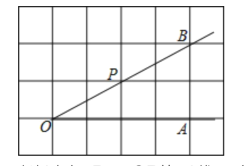
(1)过点P画OB的垂线,交OA于点E;
(2)过点P画OA的垂线,垂足为H;
(3)过点P画OA的平行线PC;
(4)若每个小正方形的边长是1,则点P到OA的距离是_________;
(5)线段PE、PH、OE的大小关系是___________(用“<"连接).
-
科目: 来源: 题型:
查看答案和解析>>【题目】当﹣2<x<2时,下列函数中,函数值y随自变量x增大而增大的有( )个.
①y=2x;②y=2﹣x;③y=﹣
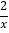 ;④y=x2+6x+8.
;④y=x2+6x+8.A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有9张卡片,分别写有1到9这就个数字,将它们的背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,若数a使关于x的不等式组
 有解,且使函数
有解,且使函数 在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )
在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )A. 10 B. 11 C. 12 D. 13
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全校学生上学的交通方式,我校九年级(21)班的5名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
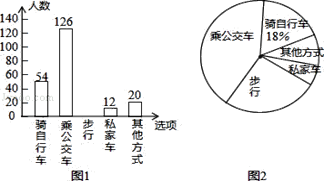
(1)本次接受调查的总人数是 人,其中“步行”的人数是 人;
(2)在扇形统计图中,“乘公交车”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由几个边长为1个单位的正方体搭成的几何体.


(1)请画出这个几何体的三视图;
(2)这个几何体的体积为______个立方单位;
(3)若保持上述正方体搭成的几何体的俯视图不变,各位置的正方体个数可以改变(正方体的总数目不变),则搭成的几何体的表面积最大为_____个平方单位.
相关试题

