【题目】如图,△ABC中,A(-2,1),B(-4,-2),C(-1,-3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′______,B′______;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△ABC的面积.

参考答案:
【答案】(1)A′(3,5)、B′(1,2);(2)作图见解析;(3)5.5.
【解析】
试题(1)由点C(-1,-3)与点C′(4,1)是对应点,得出平移规律为:向右平移5个单位,向上平移4个单位,按平移规律即可写出所求的点的坐标;
(2)按平移规律作出A、B的对应点A′,B′,顺次连接A′、B′、C′,即可得到△A′B′C′;
(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积即可求解.
试题解析:(1)∵△A′B′C′是△ABC平移之后得到的图象,并且C(-1,-3)的对应点C′的坐标为(4,1),
∴平移前后对应点的横坐标加5,纵坐标加4,
∴△ABC先向右平移5个单位,再向上平移4个单位得到△A′B′C′,
∵A(-2,1),B(-4,-2),
∴A′(3,5)、B′(1,2);
(2)△A′B′C′如图所示;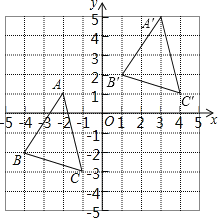
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB,作图.
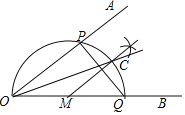
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交弧PQ 于点C;
步骤3:画射线OC.
则下列判断:①弧CQ=弧PC;②MC∥OA;③OP=PQ;④OC平分∠AOB,
其中正确的为_______________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点.沿过点E的直线折叠,使点B与点A重合,折痕现交于点F.已知EF=
 cm, 则BC的长是_______________ .
cm, 则BC的长是_______________ .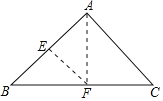
-
科目: 来源: 题型:
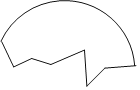
查看答案和解析>>【题目】考古学家发现了一块古代圆形陶器残片如图所示,为了修复这块陶器残片,需要找出圆心.
(1)请利用尺规作图确定这块残片的圆心O;(保留作图痕迹,不写作法)
(2)写出作图的主要依据:_______________________________________________.
-
科目: 来源: 题型:
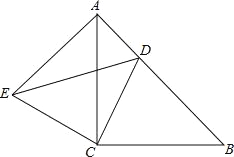
查看答案和解析>>【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地的距离为y1(km),快车离乙地的距离为y2(km),慢车的行驶时间为x(h),两车之间的距离为s(km),y1,y2与x的函数关系图象如图1所示,s与x的函数关系图象如图2所示.
(1)图中的a= ,b= .
(2)从甲地到乙地依次有E,F两个加油站,相距200km,若慢车经过E加油站时,快车恰好经过F加油站,求F加油站到甲地的距离.

-
科目: 来源: 题型:
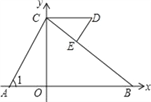
查看答案和解析>>【题目】如图,平面直角坐标系中,C(0,5)、D(a,5)(a>0),A、B在x轴上,∠1=∠D,请写出∠ACB和∠BED数量关系以及证明.
相关试题

