搜索
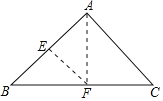
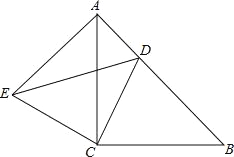
【题目】如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF=
cm， 则BC的长是_______________ ．
参考答案：
【答案】
cm
【解析】
由折叠的性质可知∠B=∠EAF=45°，所以可求出∠AFB=90°，再直角三角形的性质可知EF=
AB，所以AB、AC的长可求，再利用勾股定理即可求出BC的长．
解：∵AB=AC，∠BAC=90°，
∴∠B=∠C=45°，
∵沿过点E的直线折叠，使点B与点A重合，
∴∠B=∠EAF=45°，
∴∠AFB=90°，
∵点E为AB中点，
∴EF=AB，EF=
cm，
∴AB=AC=3 cm，
∵∠BAC=90°，
∴BC=
cm．
故答案为：cm．
-
科目： 来源： 题型：
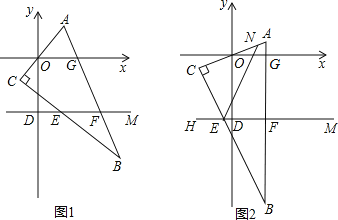
查看答案和解析>>【题目】在平面直角坐标系中，D(0，-3)，M(4，-3)，直角三角形ABC的边与x轴分别交于O、G两点，与直线DM分别交于E、F点．
(1)将直角三角形ABC如图1位置摆放，请写出∠CEF与∠AOG之间的等量关系：______．
(2)将直角三角形ABC如图2位置摆放，N为AC上一点，∠NED+∠CEF=180°，请写出∠NEF与∠AOG之间的等量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平面直角坐标系中，A（﹣3，﹣2）、B（﹣1，﹣4）
（1）直接写出：S△OAB= ；
（2）延长AB交y轴于P点，求P点坐标；
（3）Q点在y轴上，以A、B、O、Q为顶点的四边形面积为6，求Q点坐标．
-
科目： 来源： 题型：
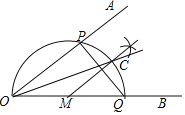
查看答案和解析>>【题目】已知∠AOB，作图．
步骤1：在OB上任取一点M，以点M为圆心，MO长为半径画半圆，分别交OA、OB于点P、Q；
步骤2：过点M作PQ的垂线交弧PQ 于点C；
步骤3：画射线OC．
则下列判断：①弧CQ=弧PC；②MC∥OA；③OP=PQ；④OC平分∠AOB，
其中正确的为_______________（填序号）
-
科目： 来源： 题型：
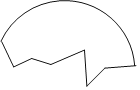
查看答案和解析>>【题目】考古学家发现了一块古代圆形陶器残片如图所示，为了修复这块陶器残片，需要找出圆心．
（1）请利用尺规作图确定这块残片的圆心O；（保留作图痕迹，不写作法）
（2）写出作图的主要依据：_______________________________________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，A(-2，1)，B(-4，-2)，C(-1，-3)，△A′B′C′是△ABC平移之后得到的图象，并且C的对应点C′的坐标为(4，1)
(1)A′、B′两点的坐标分别为A′______，B′______；
(2)作出△ABC平移之后的图形△A′B′C′；
(3)求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，
（1）求证：△ACE≌△BCD；
（2）若DE=13，BD=12，求线段AB的长．
相关试题
