【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:

(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=5m+600,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
参考答案:
【答案】(1)当电价x=600元/千度时,该工厂消耗每千度电产生利润180元/千度;
(2)当工厂每天消耗60千度电时,工厂每天消耗电产生利润为最大,最大利润为7200元.
【解析】
试题分析:(1)设y=kx+b(k≠0),利用待定系数法求一次函数解析式解答即可;
(2)根据利润=每天的用电量×每千度电产生利润y,然后整理得到W与m的关系式,再根据二次函数的最值问题解答.
解:(1)设工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为:y=kx+b,
∵该函数图象过点(0,300),(500,200),
∴![]() ,
,
解得![]() .
.
所以y=﹣0.2x+300(x≥0),
当电价x=600元/千度时,该工厂消耗每千度电产生利润y=﹣0.2×600+300=180(元/千度);
(2)设工厂每天消耗电产生利润为w元,由题意得:
w=my=m(﹣0.2x+300)
=m[﹣0.2(5m+600)+300]
=﹣m2+180m
=﹣(m﹣90)2+8100,
在m≤90时,w随m的增大而最大,
由题意,m≤60,
∴当m=60时,w最大=﹣(60﹣90)2+8100=7200,
即当工厂每天消耗60千度电时,工厂每天消耗电产生利润为最大,最大利润为7200元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,将ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么AD的长为 .

-
科目: 来源: 题型:
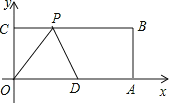
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(20,0),(0,8),点D是OA的中点,点P在BC上运动,当△ODP是以10为腰长的等腰三角形时,点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
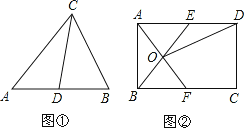
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】情景:
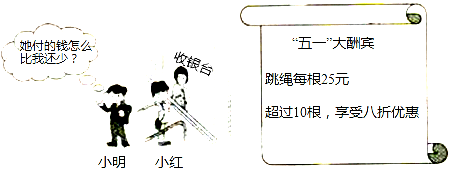
试根据图中信息,解答下列问题:
(1)购买8根跳绳需___________元,购买14根跳绳需___________元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣x﹣1=0的根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形的每个外角等于45°,则这个正多边形是( )
A. 正五边形 B. 正六边形 C. 正七边形 D. 正八边形
相关试题

