【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

参考答案:
【答案】①②④
【解析】
易证△ABD≌△EBC,可得![]()
![]() 可得①②正确,再根据角平分线的性质可求得
可得①②正确,再根据角平分线的性质可求得![]() ,即
,即![]() ,根据
,根据![]() 可求得④正确.
可求得④正确.
①BD为△ABC的角平分线,
![]()
在△ABD和△EBC中,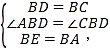
△ABD≌△EBC![]() ,
,![]() ①正确;
①正确;
②BD为△ABC的角平分线,,BD=BC,BE=BA,
![]()
△ABD≌△EBC![]()
![]()
②正确;
③
![]()
![]()
![]()
![]()
![]()
![]() 为等腰三角形,
为等腰三角形,![]() ,
,
△ABD≌△EBC,![]()
![]()
BD为△ABC的角平分线,![]() ,而EC不垂直与BC,
,而EC不垂直与BC,![]()
③错误; ④正确.
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列分式方程解应用题.
为缓解市区至通州沿线的通勤压力,北京市政府利用既有国铁线路富余能力,通过线路及站台改造,开通了“京通号”城际动车组,每班动车组预定运送乘客1200人,为提高运输效率,“京通号”车组对动车车厢进行了改装,使得每节车厢乘坐的人数比改装前多了
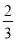 ,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
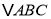 是等边三角形,点E在线段AB上,点D在直线BC上,且
是等边三角形,点E在线段AB上,点D在直线BC上,且 ,将
,将 绕点C顺时针旋转
绕点C顺时针旋转 至
至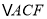 ,连接EF.
,连接EF.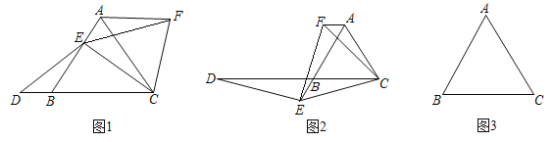
(1)证明:
 ;
;(2)如图2,如果点E在线段AB的延长线上,其他条件不变,请你写出线段AB、DB、AF之间的数量关系,并证明你的结论;
(3)如果点E在线段BA的延长线上,其他条件不变,请在图3的基础上将图形补充完整,并写出AB、DB、AF之间的数量关系,不必证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2的图象上,则a的值为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB=
 FE.
FE.
相关试题

