【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
参考答案:
【答案】(1)![]() ﹣1;(2)证明见解析
﹣1;(2)证明见解析
【解析】试题分析:(1)延长CE交AB于G,首先判断出△CAG是等腰直角三角形,然后找到∠EAB=∠CAB﹣∠CAD=30°,分别求出CG,EG即可解决问题;
(2)延长FB到H,使得BH=AF,连接EH.作EI⊥BF于I.由△ACE≌△BCE,推出AE=BE,推出∠EAB=∠EBC=30°,由△AFE≌△BHE,推出∠AFE=∠BHE,EF=EH,可得∠EFB=∠EBH=∠AFE=30°,又EI⊥FH,故在Rt△FEI中,∠EFI=30°,从而得出FI=![]() FE,可得FA+FB=
FE,可得FA+FB=![]() FE.
FE.
试题解析:解:(1)延长CE交AB于G.
∵△BAC是等腰直角三角形,CE平分∠ACB,∴CG⊥AB,∴∠AGC=90°.
∵CA=CB,∠ACB=90°,∴∠CAB=45°,∴△CAG是等腰直角三角形.
∵△BCD是等边三角形,∴BC=CD=AC,∠BCD=60°,∴∠CAD=∠CDA,∴∠ACD=∠ACB+∠BCD=150°,∴∠CAD=∠CDA=15°,∴∠EAB=∠CAB﹣∠CAD=30°.
在Rt△AEG中,∠EAG=30°,AE=2,∴AE=![]() ,EG=1.
,EG=1.
∵CG=AG=![]() ,∴CE=CG﹣EG=
,∴CE=CG﹣EG=![]() ﹣1.
﹣1.
(2)延长FB到H,使得BH=AF,连接EH.作EI⊥BF于I.
由(1)可知:AC=BC,CE平分∠ACB,∴∠ACE=∠BCE.
∵CE=CE,∴△ACE≌△BCE,∴AE=BE,∴∠EAB=∠EBC=30°.
在△AFB中,∠AFB=60°,∴∠FAB+∠FBA=120°,∴∠FAE=∠EAB+∠FAB=30°+∠FAB,∠EBH=180°﹣∠EBA﹣∠ABF=150°﹣(120°﹣∠ABF)=30°+∠FAB,∴∠EBH=∠FAE,∴△AFE≌△BHE,∴∠AFE=∠BHE,EF=EH,∴∠EFB=∠EBH=∠AFE=30°.
∵EI⊥FH,∴EI=IH,在Rt△FEI中,∠EFI=30°,∴FI= ![]() FE,∴FH=BH+FB=
FE,∴FH=BH+FB=![]() FE,∴FA+FB=
FE,∴FA+FB=![]() FE.
FE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆某油脂公司生产销售菜籽油、花生油两种食用植物油.
(1)已知花生的出油率为56%,是菜籽的1.4倍,现有菜籽、花生共100吨,若想得到至少52吨植物油,则其中的菜籽至多有多少吨?
(2)在去年的销售中,菜籽油、花生油的售价分别为20元/升,30元/升,且销量相同,今年由于花生原材料价格上涨,花生油的售价比去年提高了a%,菜籽油的售价不变,总销量比去年降低a%,且菜籽油、花生油的销量均占今年总销量的
 ,这样,预计今年的销售总额比去年下降
,这样,预计今年的销售总额比去年下降 a%,求a的值.
a%,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 开通了,中国联通公布了资费标准,其中包月
开通了,中国联通公布了资费标准,其中包月 元时,超出部分国内拨打
元时,超出部分国内拨打 元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.80
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用
 表示超出时间,
表示超出时间, 表示超出部分的电话费,那么
表示超出部分的电话费,那么 与
与 的关系式是什么?
的关系式是什么?(3)如果打电话超出
 分钟,需多付多少电话费?
分钟,需多付多少电话费?(4)某次打电话的费用超出部分是
 元,那么小明的爸爸打电话超出几分钟?
元,那么小明的爸爸打电话超出几分钟? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于12,则平移距离等于( )

A.2 B.3 C.4 D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店用1500元人民币购进某种水果销售,过了一周时间,又用3400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于900元,则每千克这种水果的标价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果把一个奇数位的自然数各数为上的数字从最高位到个位依次排列,与从个位到最高位依次排列出的一串数字完全相同,相邻两个数位上的数字之差的绝对值相等(不等于0),且该数正中间的数字与其余数字均不同,我们把这样的自然数称为“阶梯数”,例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,且|1﹣2|=|2﹣3|=|3﹣2|=|2﹣1|=1,因此12321是一个“阶梯数”,又如262,85258,…,都是“阶梯数”,若一个“阶梯数”t从左数到右,奇数位上的数字之和为M,偶数位上的数字之和为N,记P(t)=2N﹣M,Q(t)=M+N.
(1)已知一个三位“阶梯数”t,其中P(t)=12,且Q(t)为一个完全平方数,求这个三位数;
(2)已知一个五位“阶梯数”t能被4整除,且Q(t)除以4余2,求该五位“阶梯数”t的最大值与最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,
是等边三角形,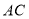 上有点D,分别以
上有点D,分别以 为边作等边
为边作等边 和等腰
和等腰 ,边
,边 、
、 交于点H,点F在
交于点H,点F在 延长线上且
延长线上且 ,连接
,连接 .求证:
.求证:
(1)
 ;
;(2)
 .
.
相关试题

