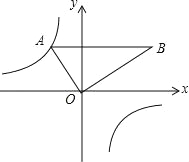
【题目】如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
(1)求双曲线的解析式;
(2)把三角板AOB绕点A顺时针旋转,使得点O的对应点C落在x轴的负半轴上的对应线段为AD,试判断点D是否在双曲线上?请说明理由.
参考答案:
【答案】(1)双曲线的解析式为y=-![]() ;(2)∴点D在双曲线上.理由见试题解析。
;(2)∴点D在双曲线上.理由见试题解析。
【解析】
试题分析:(1)如图,先求出∠AOE=30°,再根据含30度的直角三角形三边的关系求出AE和OE,从而得到A点坐标,然后利用待定系数法求反比例函数解析式;
(2)利用旋转的性质得AC=AO,∠CAO=∠BAD,则可判断△AOC为等边三角形,得到∠CAO=∠BAD=60°,于是可判断点D在AC的延长线上,然后通过证明点A与点D关于原点对称得到点D是在双曲线上.
试题解析:(1)设AB与y轴相交于点E.∵AB∥x轴,∴∠AEO=90°,
在Rt△AEO中,∠A=90°﹣30°=60°,OE=OA![]() 60°=2×
60°=2×![]() =
=![]() ,AE=OA
,AE=OA![]() °=2×
°=2×![]() =1.
=1.
∴点A的坐标为(-1,![]() ),设双曲线的解析式为y=
),设双曲线的解析式为y=![]() (k≠0),代入(-1,
(k≠0),代入(-1,![]() )可得k=
)可得k=![]() ,
,
∴双曲线的解析式为y=![]() ;
;
(2)点D是在双曲线上.理由如下:∵AB∥x轴,∴∠AOC=∠BAO=60°,∵△ACD是由△AOB绕点A旋转得到的,∴AO=AC,AB=AD,∴△AOC是等边三角形,∴∠CAO=60°,即旋转角∠BAD=∠CAO=60°,
又∠BAO=60°,∴点O在AD上,在Rt△AOB中,∠B=30°,AB=2AO,∴AD=2AO,AO=OD,
∴点D与点A关于点O中心对称.∴点D在双曲线上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一条抛物线,顶点坐标为(4,-2),且形状与抛物线y=x2+2相同,则它的函数表达式是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小刚从相距25.2千米的两地同时相向而行,小明每小时走4千米,3小时后两人相遇,设小刚的速度为x千米/时,列方程得( )
A. 4+3x=25.2
B. 3×4+x=25.2
C. 3×4+3x=25.2
D. 3x-3×4=25.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
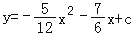 与x轴交于点A、B(点A在点B的左侧)与y轴交于点C(0,8),点D是抛物线上的动点,直线AD与y轴交于点K.
与x轴交于点A、B(点A在点B的左侧)与y轴交于点C(0,8),点D是抛物线上的动点,直线AD与y轴交于点K.(1)填空:c= ;
(2)若点D的横坐标为2,连接OD、CD、AC,以AC为直径作⊙M,试判断点D与⊙M的位置关系,并说明理由.
(3)在抛物线
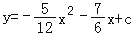 上是否存在点D,使得∠BAC=2∠BAD?若存在,试求出点D的坐标;若不存在,试说明理由.
上是否存在点D,使得∠BAC=2∠BAD?若存在,试求出点D的坐标;若不存在,试说明理由.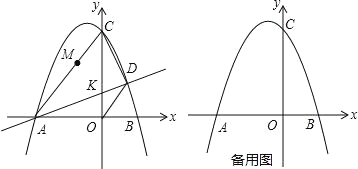
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(a,b)关于x轴的对称点P′在第三象限,那么直线y=ax+b的图象不经过( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“在△ABC中,如果∠B≠∠C,那么AB≠AC“时,应假设( )
A.AB=ACB.∠B=∠CC.AB≠ACD.∠B≠∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点 A(-1,2)关于原点的对称点是( )
A. (1,2) B. (1,-2) C. (-1,-2) D. (-1,2)
相关试题

