【题目】为了调查学生对“节约教育”内容的了解程度(程度分为:“![]() —了解很多”,“
—了解很多”,“![]() —了解较多”,“
—了解较多”,“![]() —了解较少”,“
—了解较少”,“![]() —不了解”),对某中学的部分学生进行了调查,将这次调查的结果绘制成以下两幅统计图.根据以上信息,解答下列问顾:
—不了解”),对某中学的部分学生进行了调查,将这次调查的结果绘制成以下两幅统计图.根据以上信息,解答下列问顾:
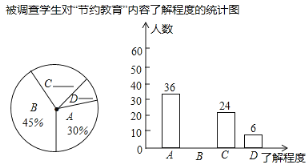
(1)本次调查了多少名学生?
(2)若该校共有1800名学生,请你估计这所学校的所有学生中,对“节约教育”内容“了解较多”的有多少名?
参考答案:
【答案】(1)120人:(2)810人.
【解析】
(1)根据总人数=任意一组的人数÷该组所占比值可知,通过条形统计图和扇形统计图找到同时出现人数和百分比重的一组数据,运用公式求解即可.
(2)本题考察了用样本估计总体,题中抽查的学生人数可看做一个样本,样本中对“节约教育”内容“了解较多”的人数所占样本的比重即大约为该校共有1800名学生中对“节约教育”内容“了解较多”的人数所占该校1800名学生的比重,通过各组人数=总人数![]() 各组所占总人数比值公式计算.
各组所占总人数比值公式计算.
(1)根据观察,只有B组同时出现人数和百分比重的数据,分别是36人占总体30%,所以
![]() 人
人
答:本次调查了120名学生.
(2)调查的样本中,B组人数占样本的45%,即用样本估计全校1800时,对“节约教育”内容“了解较多”的也大约占45%
![]() 人
人
答:估计这所学校对“节约教育”了解较多的有810名学生.
故答案为(1)120人:(2)810人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B 种纪念品可获利润30元,在(2)的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
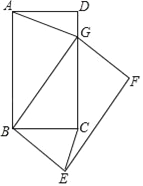
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B旋转得到矩形GBEF.
(1)观察发现:在旋转的过程中,
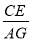 的值不变,这个数值是 ;
的值不变,这个数值是 ;(2)问题解决:当点G落在直线CD上时,求CE的长;
(3)数学思考:在旋转的过程中,CE是否有最大值,如果有,请直接写出;如果没有,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )
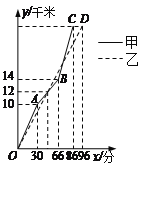
A.甲先到达终点
B.前30分钟,甲在乙的前面
C.第48分钟时,两人第一次相遇
D.这次比赛的全程是28千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的曲线是函数y=
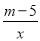 (m为常数)图象的一支.
(m为常数)图象的一支.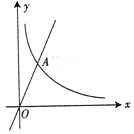
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
-
科目: 来源: 题型:
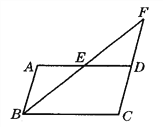
查看答案和解析>>【题目】如图,平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线交于点F.
(1)求证:△ABE≌△DFE;
(2)试连结BD,AF,判断四边形ABDF的形状,并证明你的结论.
相关试题

