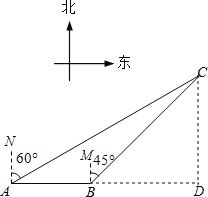
【题目】如图,大海中某岛C的周围25km范围内有暗礁.一艘海轮向正东方向航行,在A处望见C在北偏东60°处,前进20km后到达点B,测得C在北偏东45°处.如果该海轮继续向正东方向航行,有无触礁危险?请说明理由.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

参考答案:
【答案】该海轮继续向正东方向航行,无触礁危险.
【解析】试题分析:判断有无危险只要求出点C到AB的距离,与25海里比较大小就可以.首先过点C作CD⊥AB于点D,设BD=xkm,由三角函数的定义,即可求得CD=xkm,AD=![]() xkm,则可方程20+x=
xkm,则可方程20+x=![]() x,解此方程即可求得CD的长,比较即可求得答案.
x,解此方程即可求得CD的长,比较即可求得答案.
试题解析:
该海轮继续向正东方向航行,无触礁危险.
理由:过点C作CD⊥AB于点D,
∴∠BCD=∠CBM=45°,
设BD=xkm,则CD=![]() =x(km),
=x(km),
∵∠CAN=60°,
∴∠CAD=30°,
在Rt△CAD中,tan∠CAB=tan30°=![]() =
=![]() ,
,
∴AD=![]() CD=
CD=![]() x(km),
x(km),
∵AB=20km,AB+DB=AD,
∴20+x=![]() x,
x,
解得:x=10![]() +10(km),
+10(km),
∴CD=10![]() +10≈27.3(km)>25km,
+10≈27.3(km)>25km,
∴该海轮继续向正东方向航行,无触礁危险.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y﹣2与x+1成正比例函数关系,且x=﹣2时,y=6.
(1)写出y与x之间的函数关系式;
(2)求当x=﹣3时,y的值;
(3)求当y=4时,x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】n边形的每个外角都为72°,则边数n为( )
A. 5 B. 6 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市按以下规定收取每月的水费:用水不超过10立方米,按每立方米2.1元收费;如果超过10立方米,超过部分按每立方米3元收费,已知某用户l2月水费平均每立方米2.5元.
按要求回答下列问题:
(l)这个用户12月用水量____10立方米(填“超过”或“不超过”).
(2)在(1)的前提下,求12月这个用户的用水量是多少立方米?
(3)该用户12月份需交水费____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=-x-1与反比例函数y=kx-1的图象都过点A(m,1).
(1)求m的值,并求反比例函数的解析式;
(2)求正比例函数与反比例函数的另一个交点B的坐标;
(3)求△AOB的面积。
-
科目: 来源: 题型:
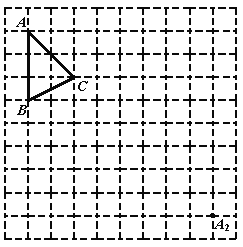
查看答案和解析>>【题目】如图,是一个由边长为1的小正方形组成的10×10的正方形网格,
(1)在网格中画出将△ABC向右平移4个单位后的△A1B1C1;
(2)△ABC绕点O旋转180°后,点A与点A2重合,请在网格中画出点O,并画出△ABC绕点O旋转180°后的△A2B2C2;
(3)描述△A1B1C1与△A2B2C2的位置关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m+1)x+2m﹣6,
(1)若函数图象过(﹣1,2),求此函数的解析式.
(2)若函数图象与直线y=2x+5平行,求其函数的解析式.
(3)求满足(2)条件的直线与直线y=﹣3x+1的交点,并求出这两条直线与y轴所围成三角形的面积.
相关试题

