【题目】已知函数y=(m+1)x+2m﹣6,
(1)若函数图象过(﹣1,2),求此函数的解析式.
(2)若函数图象与直线y=2x+5平行,求其函数的解析式.
(3)求满足(2)条件的直线与直线y=﹣3x+1的交点,并求出这两条直线与y轴所围成三角形的面积.
参考答案:
【答案】
(1)解:∵函数y=(m+1)x+2m﹣6的图象过(﹣1,2),
∴2=(m+1)×(﹣1)+2m﹣6,
解得:m=9,
故此函数的解析式为:y=10x+12
(2)解:由函数图象与直线y=2x+5平行知二者斜率相等,即m+1=2,
解得:m=1,
故函数的解析式为:y=2x﹣4
(3)解:如图,

由题意,得: ![]() ,
,
解得: ![]() ,
,
∴两直线的交点A(1,﹣2),
y=2x﹣4与y轴交点B(0,﹣4),y=﹣3x+1与y轴交点C(0,1)
∴S△ABC= ![]() ×5×1=
×5×1= ![]()
【解析】(1)将点(﹣1,2)代入函数解析式求出m即可;(2)根据两直线平行即斜率相等,即可得关于m的方程,解方程即可得;(3)联立方程组求得两直线交点坐标,再求出两直线与y轴的交点坐标,根据三角形面积公式列式计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大海中某岛C的周围25km范围内有暗礁.一艘海轮向正东方向航行,在A处望见C在北偏东60°处,前进20km后到达点B,测得C在北偏东45°处.如果该海轮继续向正东方向航行,有无触礁危险?请说明理由.(参考数据:
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=-x-1与反比例函数y=kx-1的图象都过点A(m,1).
(1)求m的值,并求反比例函数的解析式;
(2)求正比例函数与反比例函数的另一个交点B的坐标;
(3)求△AOB的面积。
-
科目: 来源: 题型:
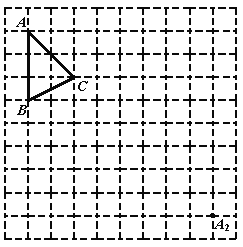
查看答案和解析>>【题目】如图,是一个由边长为1的小正方形组成的10×10的正方形网格,
(1)在网格中画出将△ABC向右平移4个单位后的△A1B1C1;
(2)△ABC绕点O旋转180°后,点A与点A2重合,请在网格中画出点O,并画出△ABC绕点O旋转180°后的△A2B2C2;
(3)描述△A1B1C1与△A2B2C2的位置关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别
频数(人数)
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
1
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M,N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2a5+t= a2t ,则t= ________.
相关试题

