【题目】已知如图抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C(0,﹣3)
(1)请直接写出抛物线的解析式.
(2)抛物线的对称轴上是否存在一点P,使得△ACP的周长最短,若存在,请直接写出点P的坐标.
(3)点G的坐标是(2,﹣3),点F是x轴上一点,抛物线上是否存在点R,使得以A,G,F,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标.
(4)在B、C连线的下方抛物线上是否存在一点Q,使得△QBC的面积是△ABC的面积的一半?若存在,求出点Q的坐标.
(5)抛物线的顶点设为D,对称轴与y轴的交点为E,M(m,0)是x轴上一动点,点N是线段DE上的一点,若∠MNC=90°,请直接写出实数m的变化范围.
参考答案:
【答案】
(1)解:∵抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0),
∴y=a(x+1)(x﹣3),
把点C(0,﹣3)代入y=a(x+1)(x﹣3)得,a=1,
∴抛物线的解析式为;y=x2﹣2x﹣3
(2)解:存在,如图1
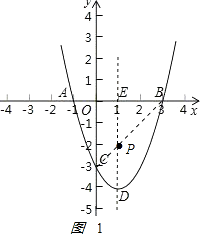 ,
,
连接BC交对称轴于P,
则PA+PC=BC最短,
即△ACP的周长最短,
设直线BC的解析式为:y=kx+b,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线BC的解析式为:y=x﹣3,
∵抛物线的对称轴是直线x=1,
把x=1代入y=x﹣3,
得y=﹣2,
∴P(1,﹣2)
(3)解:存在点R,使得以A,G,F,R为顶点的四边形是平行四边形,
①平行四边形ARGF时,RG∥AF,yR=yG=﹣3,
当y=﹣3时,x2﹣2x﹣3=﹣3,解得x1=0,x2=2(舍)
点R1(0,﹣3);
②平行四边形AGFR时,yR+yG=0,即yR=3,当y=3时,x2﹣2x﹣3=3,解得x1=1﹣ ![]() ,x2=1+
,x2=1+ ![]() ,
,
R2(1﹣ ![]() ,3 ),R3(1+
,3 ),R3(1+ ![]() ,3),
,3),
综上所述:存在,点R的坐标(0,﹣3),(1﹣ ![]() ,3 ),(1+
,3 ),(1+ ![]() ,3)
,3)
(4)解:如图2
 ,
,
连BC,直线BC解析式为y=x﹣3,△ABC面积可求得6.
△ABC与△QBC同底,
则底BC上的高应为 ![]() ,
,
过点C,作CQ⊥BC,则CQ= ![]() ,再过Q作QH⊥y轴与H,
,再过Q作QH⊥y轴与H,
由Rt△CHQ∽△COB,得Q(1,﹣4),过Q作直线QL∥BC,
直线QL解析式可求得y=x﹣5,
联立方程组,得 ![]() ,
,
解得 ![]() ,
, ![]() ,
,
所以在BC连线下方的抛物线上存在这点Q1(1,﹣4)Q2(2,﹣3)使得△QBC是△ABC面积的一半
(5)解:如图3
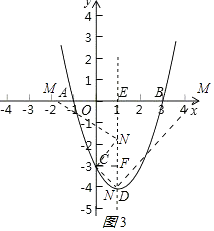 ,
,
①作∠MNC=90°,过点C做CF⊥DE,则△CFN∽△NEM,得
![]() .
.
设NE=n,M(m,0),D(1,﹣4),C(0,﹣3),
则CF=1,NE=n,FN=3﹣n,ME=1﹣m,
代入比例式,得
一元二次方程n2﹣3n+(1﹣m)=0 关于n的一元二次方程有解,
则m≥﹣ ![]() ;
;
②当点N移动到点D时,△CNF是等腰直角三角形,与△ENM仍然相似,
所以EM=EN=4,
所以此时m=5,
综上可知 m的范围是﹣ ![]() ≤m≤5
≤m≤5
【解析】(1)根据待定系数法,可得答案;(2)根据轴对称的性质,可得A、B关于对称轴对称,根据线段的性质可得答案;(3)根据平行四边形的性质可得答案;(4)根据面积可得CQ的长度,根据平行线的性质,可得QL,根据解方程组可得答案;(5)根据相似三角形的性质,可得关于n的方程,根据方程跟的判别式可得答案,再根据相似三角形的性质可得答案。
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC,CD交于点M、N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是;
(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 从原点出发沿数轴向左运动,同时点
从原点出发沿数轴向左运动,同时点 也从原点出发沿数轴向右运动,
也从原点出发沿数轴向右运动, 秒后,两点相距
秒后,两点相距 个单位长度,已知点
个单位长度,已知点 的速度是点
的速度是点 的速度的
的速度的 倍(速度单位:单位长度/秒).
倍(速度单位:单位长度/秒).
(1)求出点
 、点
、点 运动的速度,并在数轴上标出
运动的速度,并在数轴上标出 ,
, 两点从原点出发运动
两点从原点出发运动 秒时的位置.
秒时的位置.(2)若
 ,
, 两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点
两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点 、点
、点 的正中间?
的正中间? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 中,
中, 平分
平分 ,交
,交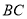 于点
于点 ,且
,且 ,延长
,延长 与
与 的延长线交于点
的延长线交于点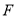 ,连接
,连接 ,
, .下列结论:①
.下列结论:① ;②
;② 是等边三角形;③
是等边三角形;③ ;④
;④ ;⑤
;⑤ 中正确的有( )
中正确的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?A,B两款手机的进货和销售价格如下表:
A款手机
B款手机
进货价格(元)
1100
1400
销售价格(元)
今年的销售价格
2000
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图中给出的信息,回答下列问题:
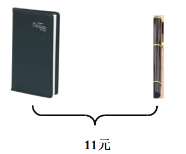

(1)一本笔记本与一支中性笔分别是多少元?
(2)某学校给参加体育比赛获一等奖的10名学生发笔记本,给获二等奖的20名学生发中性笔,现有两个超市在搞促销活动,A超市规定:这两种商品都打八折;B超市规定:每买一个笔记本送一支中性笔,另外购买的中性笔按原价卖.该学校选择哪家超市购买更合算,并说明理由.
相关试题

