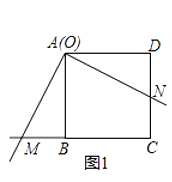
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC,CD交于点M、N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是;
(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)
参考答案:
【答案】
(1)OM=ON
(2)解:仍成立.
证明:如图2,连接AC,BD,
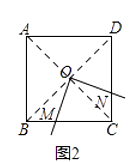
则由正方形ABCD可得,∠BOC=90°,BO=CO,∠OBM=∠OCN=45°
∵∠MON=90°
∴∠BOM=∠CON
在△BOM和△CON中
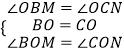
∴△BOM≌△CON(ASA)
∴OM=ON
(3)解:如图3,过点O作OE⊥BC,作OF⊥CD,垂足分别为E、F,
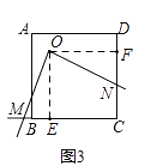
则∠OEM=∠OFN=90°
又∵∠C=90°
∴∠EOF=90°=∠MON
∴∠MOE=∠NOF
在△MOE和△NOF中
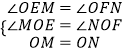
∴△MOE≌△NOF(AAS)
∴![]() OE=OF
OE=OF
又∵OE⊥BC,OF⊥CD
∴点O在∠C的平分线上
∴O在移动过程中可形成线段AC
(4)解:O在移动过程中可形成直线AC
【解析】解:(1)若点O与点A重合,则OM与ON的数量关系是:OM=ON;
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某人到一家快递公司办理环江香米(简称香米)的快递托运,重量为
 千克.快递公司收取托运费方案如下:
千克.快递公司收取托运费方案如下:凡物品重量不超过10千克的,按2元/千克收取托运费;当物品重量超过10千克的,超出部分按3元/千克加收托运费.
(1)写出
 千克香米的托运费的表达式 (用含字母
千克香米的托运费的表达式 (用含字母 的式子表示);
的式子表示);(2)若托运香米重量为
 千克时,求出这笔托运费.
千克时,求出这笔托运费. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 从原点出发沿数轴向左运动,同时点
从原点出发沿数轴向左运动,同时点 也从原点出发沿数轴向右运动,
也从原点出发沿数轴向右运动, 秒后,两点相距
秒后,两点相距 个单位长度,已知点
个单位长度,已知点 的速度是点
的速度是点 的速度的
的速度的 倍(速度单位:单位长度/秒).
倍(速度单位:单位长度/秒).
(1)求出点
 、点
、点 运动的速度,并在数轴上标出
运动的速度,并在数轴上标出 ,
, 两点从原点出发运动
两点从原点出发运动 秒时的位置.
秒时的位置.(2)若
 ,
, 两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点
两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点 、点
、点 的正中间?
的正中间? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C(0,﹣3)

(1)请直接写出抛物线的解析式.
(2)抛物线的对称轴上是否存在一点P,使得△ACP的周长最短,若存在,请直接写出点P的坐标.
(3)点G的坐标是(2,﹣3),点F是x轴上一点,抛物线上是否存在点R,使得以A,G,F,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标.
(4)在B、C连线的下方抛物线上是否存在一点Q,使得△QBC的面积是△ABC的面积的一半?若存在,求出点Q的坐标.
(5)抛物线的顶点设为D,对称轴与y轴的交点为E,M(m,0)是x轴上一动点,点N是线段DE上的一点,若∠MNC=90°,请直接写出实数m的变化范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 中,
中, 平分
平分 ,交
,交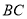 于点
于点 ,且
,且 ,延长
,延长 与
与 的延长线交于点
的延长线交于点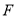 ,连接
,连接 ,
, .下列结论:①
.下列结论:① ;②
;② 是等边三角形;③
是等边三角形;③ ;④
;④ ;⑤
;⑤ 中正确的有( )
中正确的有( )
A.1个B.2个C.3个D.4个
相关试题

