【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①;cos(α+β)=cosαcosβ﹣sinαsinβ②;tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,
如:tan105°=tan(45°+60°)=![]() =
=![]() =
=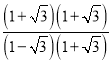 =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
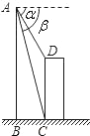
参考答案:
【答案】建筑物CD的高为84米.
【解析】试题分析:先由俯角β的正切值及BC求得AB,再由俯角α的正切值及BC求得A、D两点垂直距离.CD的长由二者相减即可求得.
试题解析:由于α=60°,β=75°,BC=42,
则AB=BCtanβ=42tan75°=42×![]() =42×
=42×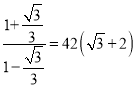 ,
,
A、D垂直距离为BCtanα=42![]() ,
,
∴CD=AB﹣42![]() =84(米).
=84(米).
答:建筑物CD的高为84米.
-
科目: 来源: 题型:
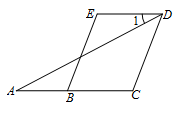
查看答案和解析>>【题目】已知:如图,BE//CD , ∠A=∠1. 求证:∠C=∠E .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区注重城市绿化提高市民生活质量,新建林荫公园计划购买甲、乙两种树苗共800株,甲种树苗每株12元,乙种树苗每株15元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去10500元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“a<b”的反面应是( )
A.a≠b B.a>b C.a=b D.a=b或a>b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(2,3),B(6,3),连结AB,如果点P在直线y=x﹣1上,且点P到直线AB的距离小于1,那么称点P是线段AB的“邻近点”.

(1)判断点C( ,
,  )是否是线段AB的“邻近点” .
)是否是线段AB的“邻近点” .
(2)若点Q(m,n)是线段AB的“邻近点”,则m的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x﹣1)(2x+1)﹣(x2+x﹣2)的结果,与下列哪一个式子相同( )
A.x2﹣2x﹣3
B.x2﹣2x+1
C.x2+x﹣3
D.x2﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2﹣3x= .
相关试题

