【题目】如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为 . 
参考答案:
【答案】2
【解析】解:将△DAF绕点A顺时针旋转90度到△BAF′位置, 由题意可得出:△DAF≌△BAF′,
∴DF=BF′,∠DAF=∠BAF′,
∴∠EAF′=45°,
在△FAE和△EAF′中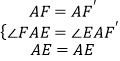 ,
,
∴△FAE≌△EAF′(SAS),
∴EF=EF′,
∵△ECF的周长为4,
∴EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=4,
∴2BC=4,
∴BC=2.
故答案为:2.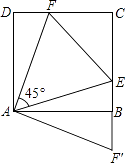
根据旋转的性质得出∠EAF′=45°,进而得出△FAE≌△EAF′,即可得出EF+EC+FC=FC+CE+EF′=FC+BC+BF′=4,得出正方形边长即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果两个一元一次方程的解互为相反数,我们就称这两个方程为“兄弟方程”.
如方程2x=4和3x+6=0为“兄弟方程”.
(1)若关于x的方程5x+m=0与方程2x﹣4=x+1是“兄弟方程”,求m的值;
(2)若两个“兄弟方程”的两个解的差为8,其中一个解为n,求n的值;
(3)若关于x的方程2x+3m﹣2=0和3x﹣5m+4=0是“兄弟方程”,求这两个方程的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,点B是数轴上原点O两侧的两点,其中点A在负半轴上,且满足AB=12,OB=2OA.
(1)点A,B在数轴上对应的数分别为 和 ;
(2)点A,B同时分别以每秒2个单位长度和每秒4个单位长度的速度向左运动.
①经过几秒后,OA=3OB;
②点A,B在运动的同时,点P以每秒2个单位长度的速度从原点向右运动,经过几秒后,点A,B,P中的某一点成为其余两点所连线段的中点.

-
科目: 来源: 题型:
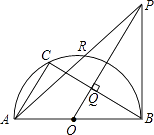
查看答案和解析>>【题目】如图,AB是半圆O的直径,C是半圆O上一点,OQ⊥BC于点Q,过点B作半圆O的切线,交OQ的延长线于点P,PA交半圆O于R,则下列等式中正确的是( )
A.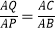
B.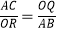
C.
D.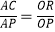
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若AD=6,AB=14,请求出CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:(2014﹣ )0+|3﹣
)0+|3﹣  |﹣
|﹣ 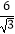 ;
;
(2)化简:(1﹣ )÷(
)÷(  ﹣2)
﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,CD⊥AD于点D,点E,A,D在同一直线上,且∠ACD=35°,求∠BAE的度数.

相关试题

