【题目】如图,在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,CD⊥AD于点D,点E,A,D在同一直线上,且∠ACD=35°,求∠BAE的度数.

参考答案:
【答案】59°
【解析】
设∠BAC为3x度,∠BCA为2x度,在△BAC中,利用三角形内角和定理求得∠BAC和∠DAC,在△ACD中利用三个角的和定理求∠DAC,因为∠EAD为平角,用180°-∠DAC-∠BAC即可得∠BAE的度数.
在△ABC中,
因为∠BAC∶∠BCA=3∶2,
所以可设∠BAC=3x°,∠BCA=2x°.
因为∠B+∠BAC+∠BCA=180°,∠B=70°,
所以70+3x+2x=180,所以x=22,
所以∠BAC=3×22°=66°.
又因为CD⊥AD,
所以∠D=90°,
所以∠CAD+∠ACD=90°,
所以∠CAD=90°-∠ACD=90°-35°=55°.
因为∠DAE是平角,
所以∠BAE=180°-∠BAC-∠CAD=180°-66°-55°=59°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若AD=6,AB=14,请求出CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:(2014﹣ )0+|3﹣
)0+|3﹣  |﹣
|﹣ 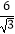 ;
;
(2)化简:(1﹣ )÷(
)÷(  ﹣2)
﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
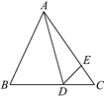
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川省“单独两孩”政策于2014年3月20日正式开始实施,该政策的实施可能给我们的生活带来一些变化,绵阳市人口计生部门抽样调查了部分市民(每个参与调查的市民必须且只能在以下6种变化中选择一项),并将调查结果绘制成如下统计图:
种类
A
B
C
D
E
F
变化
有利于延缓社会老龄化现象
导致人口暴增
提升家庭抗风险能力
增大社会基本公共服务的压力
缓解男女比例不平衡现象
促进人口与社会、资源、环境的协调可持续发展

根据统计图,回答下列问题:
(1)参与调查的市民一共有人;
(2)参与调查的市民中选择C的人数是人;
(3)∠α=;
(4)请补全条形统计图. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点M为直线AB上一动点,
 都是等边三角形,连接BN
都是等边三角形,连接BN  求证:
求证:  ;
; 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系 不需证明
不需证明 ;
; 如图4,当
如图4,当 时,证明:
时,证明:  .
.
相关试题

