【题目】已知∠A的两边与∠B的两边分别平行,且∠A比∠B的3倍少40°,那么∠A=______°.
参考答案:
【答案】20°或125°
【解析】
设∠B的度数为x,则∠A的度数为3x-40°,根据两边分别平行的两个角相等或互补得到x=3x-40°或x+3x-40°=180°,再分别解方程,然后计算3x-40°的值即可.
解:设∠B的度数为x,则∠A的度数为3x-40°,
当∠A=∠B时,即x=3x-40°,解得x=20°,
∴∠A=20°;
当∠A+∠B=180°时,即x+3x-40°=180°,解得x=55°,
∴∠A=125°;
即∠A的度数为20°或125°.
故答案为:20°或125°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1 , ∠ABD1与∠ACD1的角平分线交于点D2 , 依此类推,∠ABD4与∠ACD4的角平分线交于点D5 , 则∠BD5C的度数是( )

A.56°
B.60°
C.68°
D.94° -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3a3a2﹣2a7÷a2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和BC′F的周长之和为( )
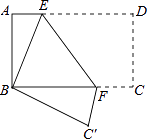
A.3
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
(1)求证:CE=CB;
(2)若AC=
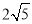 ,CE=
,CE=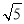 ,求AE的长.
,求AE的长.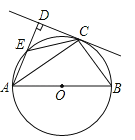
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:b(2a+5b)+a(3a﹣2b)=
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3 . 若正方形EFGH的边长为2,则S1+S2+S3= .

相关试题

