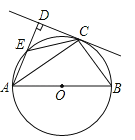
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
(1)求证:CE=CB;
(2)若AC=![]() ,CE=
,CE=![]() ,求AE的长.
,求AE的长.
参考答案:
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)连接OC,利用切线的性质和已知条件推知OC∥AD,根据平行线的性质和等角对等边证得结论;
(2)AE=AD﹣ED,通过相似三角形△ADC∽△ACB的对应边成比例求得AD=4,DC=2.在直角△DCE中,由勾股定理得到DE=![]() =1,故AE=AD﹣ED=3.
=1,故AE=AD﹣ED=3.
试题解析:(1)证明:连接OC,∵CD是⊙O的切线,∴OC⊥CD.
∵AD⊥CD,∴OC∥AD,∴∠1=∠3.
又OA=OC,∴∠2=∠3,∴∠1=∠2,∴CE=CB;
(2)解:∵AB是直径,∴∠ACB=90°,∵AC=![]() ,CB=CE=
,CB=CE=![]() ,∴AB=
,∴AB=![]() =
=![]() =5.∵∠ADC=∠ACB=90°,∠1=∠2,∴△ADC∽△ACB,∴
=5.∵∠ADC=∠ACB=90°,∠1=∠2,∴△ADC∽△ACB,∴![]() ,即
,即![]() ,∴AD=4,DC=2.在直角△DCE中,DE=
,∴AD=4,DC=2.在直角△DCE中,DE=![]() =1,∴AE=AD﹣ED=4﹣1=3.
=1,∴AE=AD﹣ED=4﹣1=3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3a3a2﹣2a7÷a2= .
-
科目: 来源: 题型:
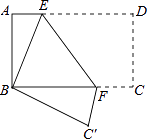
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和BC′F的周长之和为( )
A.3
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A的两边与∠B的两边分别平行,且∠A比∠B的3倍少40°,那么∠A=______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:b(2a+5b)+a(3a﹣2b)=
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3 . 若正方形EFGH的边长为2,则S1+S2+S3= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=
 BC,则△ABC的顶角的度数为 .
BC,则△ABC的顶角的度数为 .
相关试题

