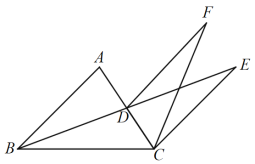
【题目】如图,![]() 是
是![]() 中
中![]() 边上的中线,过点
边上的中线,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 为
为![]() 外一点,连接
外一点,连接![]() ,且
,且![]() .求证:
.求证:
(1)![]() ;
;
(2)CA平分![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)根据中线得AD=DC,根据平行线得∠A=∠DCE,∠ABD=∠E,进而根据“AAS”即可得证;
(2)由(1)可得BD=DE,结合DE=DF可得BD=DF,根据等角的补角相等可得∠CDF=∠CDB,进而根据“SAS”可得△CDF≌△CDB,进而得到∠DCF=∠DCB即可得证.
证明:(1)∵BD是△ABC的中线,
∴AD=DC,
∵CE∥AB,
∴∠A=∠DCE,∠ABD=∠E,
在△ABD与△CED中,
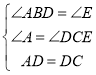
∴△ABD≌△CED(AAS),
(2)∵△ABD≌△CED,
∴BD=DE,
∵DE=DF,
∴BD=DF,
∵∠ADF=∠CDE,∠ADF+∠CDF=180°,∠CDE+∠CDB=180°,
∴∠CDF=∠CDB,
在△CDF与△CDB中,
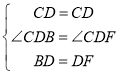
∴△CDF≌△CDB(AAS),
∴∠DCF=∠DCB,
∴CA平分∠BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2mx﹣3m2(m>0)与x轴交于A、B两点,A点在B点左边,与y轴交于C点,顶点为M.
(1)当m=1时,求点A、B、M坐标;
(2)如图(1)的条件下,若P为抛物线上一个动点,以AP为斜边的等腰直角的直角顶点Q在对称轴上,(A、P、Q按顺时针方向排列),求P点坐标.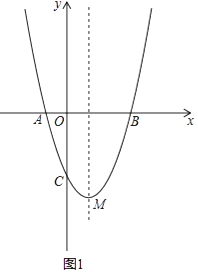
(3)如图2,若一次函数y=kx+b过B点且与抛物线只有一个公共点,平移直线y=kx+b,使其过抛物线的顶点M,与抛物线另一个交点为D,与x轴交于F点,当m变化时,求证:DF:MF是定值.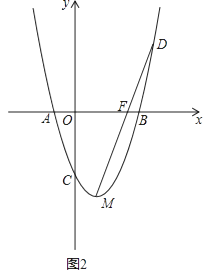
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 于
于
 且
且 则
则 的长度是( )
的长度是( )
A. 3B. 5C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】《重庆市生活垃圾分类管理办法》于2019年开始实施我校为积极响应政府对垃圾分类处理的号召,开展了垃圾分类网上知识竞赛,并从该校七年级随机抽取了部分学生的竞赛成绩进行整理、描述和分析(根据成绩共分
 四个等级),其中获得
四个等级),其中获得 等级和
等级和 等级的人数相等.
等级的人数相等.下面给出了相应的条形统计图和扇形统计图:

根据以上信息,解答下列问题:
(1)共抽取了______名学生;
(2)补全条形统计图,并求出扇形统计图中
 等级对应的圆心角的度数;
等级对应的圆心角的度数;(3)A等级中有
 名同学是女生,学校计划从
名同学是女生,学校计划从 等级的学生中抽取
等级的学生中抽取 名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少?
名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】玲玲和牛牛相约在小区笔直的步行道上健步走锻炼身体.两人都从步行道起点
 向终点
向终点 走去.牛牛出发
走去.牛牛出发 分钟后,玲玲出发.又过了
分钟后,玲玲出发.又过了 分钟,牛牛停下来接了
分钟,牛牛停下来接了 分钟的电话,玲玲则以原速继续步行,与牛牛相遇后,玲玲的速度减少到原来的
分钟的电话,玲玲则以原速继续步行,与牛牛相遇后,玲玲的速度减少到原来的 走向终点
走向终点 .牛牛接完电话后,提高速度向终点
.牛牛接完电话后,提高速度向终点 走去,
走去, 分钟后刚好追上玲玲,到达终点
分钟后刚好追上玲玲,到达终点 后立即调头以提速后的速度返回起点
后立即调头以提速后的速度返回起点 (调头时间忽略不计),玲玲、牛牛两人相距的路程
(调头时间忽略不计),玲玲、牛牛两人相距的路程 (米)与牛牛出发的时间
(米)与牛牛出发的时间 (分钟)之间的关系如图所示.
(分钟)之间的关系如图所示.
(1)牛牛开始健步走的速度为_______米/分;
(2)求玲玲开始健步走的速度和牛牛提速后的速度;
(3)玲玲走到终点
 后,停下来休息了一会儿.牛牛回到起点
后,停下来休息了一会儿.牛牛回到起点 后,立即调头仍以提速后的速度走向终点
后,立即调头仍以提速后的速度走向终点 ,玲玲休息
,玲玲休息 分钟后以减速后的速度调头走向起点
分钟后以减速后的速度调头走向起点 两人恰好在
两人恰好在 中点处相遇,求步行道
中点处相遇,求步行道 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,运算结果正确的是( )
A.(﹣1)3+(﹣3.14)0+2﹣1=﹣
B.2x﹣2=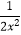
C.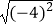 =﹣4
=﹣4
D.a2a3=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 且
且 点在线段
点在线段 上,连接
上,连接 .
.(1)如图1,若
 求线段
求线段 的长;
的长;
(2)如图1,若
 求证:
求证:
(3)如图2,在第(2)问的条件下,若点
 在
在 的延长线上时,连接
的延长线上时,连接 的面积为
的面积为 的面积为
的面积为 的面积为
的面积为 .直接写出
.直接写出 之间的数量关系.
之间的数量关系.
相关试题

