【题目】抛物线y=x2﹣2mx﹣3m2(m>0)与x轴交于A、B两点,A点在B点左边,与y轴交于C点,顶点为M.
(1)当m=1时,求点A、B、M坐标;
(2)如图(1)的条件下,若P为抛物线上一个动点,以AP为斜边的等腰直角的直角顶点Q在对称轴上,(A、P、Q按顺时针方向排列),求P点坐标.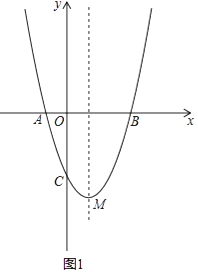
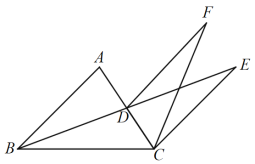
(3)如图2,若一次函数y=kx+b过B点且与抛物线只有一个公共点,平移直线y=kx+b,使其过抛物线的顶点M,与抛物线另一个交点为D,与x轴交于F点,当m变化时,求证:DF:MF是定值.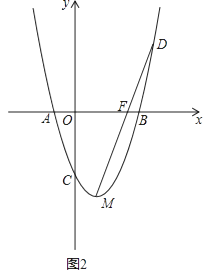
参考答案:
【答案】
(1)解:当m=1时,抛物线解析式为y=x2﹣2x﹣3,
当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0);
∵y=(x﹣1)2﹣4,
∴M点坐标为(1,﹣4);
(2)解:抛物线的对称轴为直线x=1,直线x=1交x轴于N,设P(t,t2﹣2t﹣3),Q(1,a)
作PH⊥直线x=1于点H,如图,
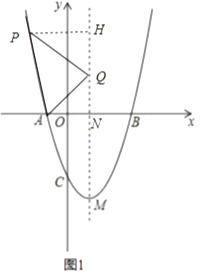
∵△APQ为等腰直角三角形,
∴PQ=AQ,∠AQP=90°,
∵∠AQH+∠AQN=90°,∠AQN+∠QAN=90°,
∴∠PQH=∠QAN,
在△PQH和△QAN中
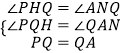 ,
,
∴△PQH≌△QAN,
∴QH=AN,PH=QN,
即t2﹣2t﹣3﹣a=2,1﹣t=a,
∴t2﹣2t﹣3﹣(1﹣t)=2,
整理得t2﹣t﹣5=0,解得t1= ![]() ,t2=
,t2= ![]() ,
,
∴P点坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() );
);
(3)解:证明:y=x2﹣2mx﹣3m2=(x﹣m)2﹣4m2,则M(m,﹣4m2),
当y=0时,x2﹣2mx﹣3m2=0,解得x1=﹣m,x2=3m,则B(3m,0),
把B(3m,0)代入y=kx+b得3mk+b=0,解得b=﹣3mk,
则直线y=kx+b的解析式表示为y=kx﹣3mk,
∵一次函数y=kx﹣3mk与抛物线只有一个公共点,
∴方程x2﹣2mx﹣3m2=kx﹣3mk有相等的实数解,
方程整理为x2﹣(2m+k)x﹣3m2+3mk=0,
∵△=(2m+k)2﹣4(﹣3m2+3mk)=0,
∴k=4m,
∴一次函数y=kx+b表示为y=4mx﹣12m2,
设直线y=kx+b平移后的解析式为y=4mx+n,
把M(m,﹣4m2)代入得﹣4m2=﹣4m2+n,解得n=﹣8m2,
即经过点D的直线解析式为y=4mx﹣8m2,
当y=0时,4mx﹣8m2=0,解得x=2m,则F(2m,0)
解方程组 ![]() 得
得 ![]() 或
或 ![]() ,则D(5m,12m2)
,则D(5m,12m2)
作AG⊥x轴于E,MG∥x轴,它们相交于点G,如图2,

∵EF∥MG,
∴ ![]() =
= ![]() =
= ![]() =3.
=3.
【解析】(1)把m=1代入得到抛物线的解析式,然后利用配方法可求得点M的坐标,接下来,令y=0可求得对应的x的值,从而可得到点A和点B的坐标;
(2)设P(t,t2﹣2t﹣3),Q(1,a),作PH⊥直线x=1于点H,首先证明△PQH≌△QAN,依据全等三角形的性质可得到QH=AN,PH=QN,从而可得到关于a、t的方程组,解方程组可求得点P的坐标;
(3)作AG⊥x轴于E,MG∥x轴,它们相交于点G,利用配方法求得抛物线的顶点坐标为M(m,﹣4m2),然后令y=0可求得B(3m,0),把B(3m,0)代入y=kx+b得3mk+b=0,求得b的值,从而得直线的解析式为y=kx﹣3mk,接下来,将y=kx﹣3mk代入抛物线的解析式,得到关于x的方程,然后由一次函数y=kx﹣3mk与抛物线只有一个公共点可得到△=0,从而可得到k与m的关系,设直线y=kx+b平移后的解析式为y=4mx+n,把点M的坐标代入可得到n=﹣8m2,则经过点D的直线解析式为y=4mx﹣8m2,然后再求得点F的坐标,解方程组可求得点D的坐标,最后,依据平行线分线段成比例定理求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,可以得到
 .
.
(1)画出平移后的
 ;
; (2)写出
 三个顶点的坐标;
三个顶点的坐标;(3)已知点P在x轴上,以
 、
、 、P为顶点的三角形面积为4,求点P的坐标.
、P为顶点的三角形面积为4,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12
 D. 16
D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家快餐店销售
 三种套餐,其中
三种套餐,其中 套餐包含一荤两素,
套餐包含一荤两素, 套餐包含两荤一素,
套餐包含两荤一素, 套餐包含两荤两素,每份套餐中一荤的成本相同,一素的成本也相同,已知一份
套餐包含两荤两素,每份套餐中一荤的成本相同,一素的成本也相同,已知一份 套餐的售价是一份
套餐的售价是一份 套餐和一份
套餐和一份 套餐售价之和的
套餐售价之和的 一天下来,店长发现
一天下来,店长发现 套餐和
套餐和 套餐的销量相同,且
套餐的销量相同,且 套餐的利润和是
套餐的利润和是 套餐利润的两倍,当天的总利润率是
套餐利润的两倍,当天的总利润率是 .第二天店内搞活动,
.第二天店内搞活动, 套餐的售价打五折,
套餐的售价打五折, 套餐的售价均不变,当
套餐的售价均不变,当 三种套餐的销量相同时,总利润率为________.
三种套餐的销量相同时,总利润率为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 于
于
 且
且 则
则 的长度是( )
的长度是( )
A. 3B. 5C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】《重庆市生活垃圾分类管理办法》于2019年开始实施我校为积极响应政府对垃圾分类处理的号召,开展了垃圾分类网上知识竞赛,并从该校七年级随机抽取了部分学生的竞赛成绩进行整理、描述和分析(根据成绩共分
 四个等级),其中获得
四个等级),其中获得 等级和
等级和 等级的人数相等.
等级的人数相等.下面给出了相应的条形统计图和扇形统计图:

根据以上信息,解答下列问题:
(1)共抽取了______名学生;
(2)补全条形统计图,并求出扇形统计图中
 等级对应的圆心角的度数;
等级对应的圆心角的度数;(3)A等级中有
 名同学是女生,学校计划从
名同学是女生,学校计划从 等级的学生中抽取
等级的学生中抽取 名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少?
名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
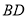 是
是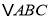 中
中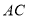 边上的中线,过点
边上的中线,过点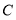 作
作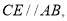 交
交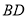 的延长线于点
的延长线于点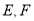 为
为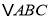 外一点,连接
外一点,连接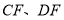 ,且
,且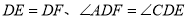 .求证:
.求证:(1)
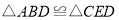 ;
;(2)CA平分
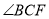 .
.
相关试题

