【题目】如图1,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.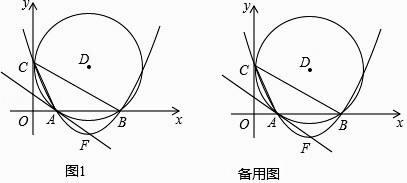
(1)D点的坐标是 , 圆的半径为;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大面积是多少?并求出N点坐标.
参考答案:
【答案】
(1)(5,4);5
(2)
解:如图1所示:
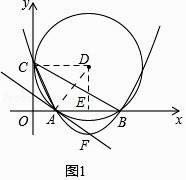
∵D(5,4),
∴E(5,0).
∴A(2,0)、B(8,0).
设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入得:16a=4,解得:a= ![]() ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+4.
x+4.
(3)
解:∵y= ![]() x2﹣
x2﹣ ![]() x+4,
x+4,
∴抛物线的顶点坐标F(5,﹣ ![]() ).
).
∴DF=4+ ![]() =
= ![]() ,AF=
,AF= ![]() =
= ![]() .
.
又∵AD=5.
∴AD2+AF2=DF2,
∴△DAF为直角三角形.
∴∠DAF=90°.
∴AF是⊙D的切线.
(4)
解:如图2所示:过点N作NP∥y轴,交BC与点P.
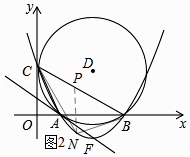
设BC的解析式为y=kx+4,将点B的坐标代入得:8k+4=0,解得k=﹣ ![]() .
.
∴BC的解析式为y=﹣ ![]() x+4.
x+4.
设N点坐标(a, ![]() a2﹣
a2﹣ ![]() a+4),则点P坐标为(a,﹣
a+4),则点P坐标为(a,﹣ ![]() a+4).
a+4).
∴NP=﹣ ![]() a+4﹣(
a+4﹣( ![]() a2﹣
a2﹣ ![]() a+4)=﹣
a+4)=﹣ ![]() a2+2a.
a2+2a.
∴S△ABC=S△CPN+S△PBN= ![]() ×BO×PN=
×BO×PN= ![]() ×8×(﹣
×8×(﹣ ![]() a2+2a)=﹣(a﹣4)2+16.
a2+2a)=﹣(a﹣4)2+16.
∴当a=4时,S△ABC最大,最大值为16,此时,N(4,﹣2).
【解析】解:(1)连接CD,过点D作DE⊥AB,垂足为E,连接AD.
∵DE⊥AB,
∴AE= ![]() AB=3.
AB=3.
∵⊙D与y轴相切,
∴DC⊥y轴.
∵∠COE=∠OED=∠OCD=90°,
∴四边形OCDE为矩形.
∴OC=DE.
∵C(0,4),
∴DE=4.
在Rt△AED中,AD= ![]() =5.
=5.
∴⊙D的半径为5.
∴D(5,4).
所以答案是:(5,4),5.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 , ∠CAC′=°.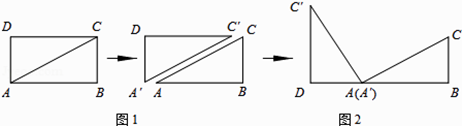
(2)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.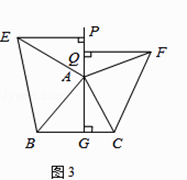
(3)如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,说明理由.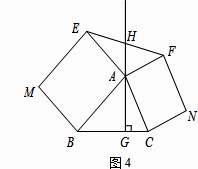
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, 、
、 的平分线交于
的平分线交于 ,
, 是
是 延长线上一点,且
延长线上一点,且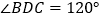 .下列结论:①
.下列结论:①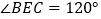 ;②
;② ;③
;③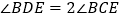 .其中所有正确结论的序号有( ).
.其中所有正确结论的序号有( ).
A. ①② B. ①③ C. ②③ D. ①②③
-
科目: 来源: 题型:
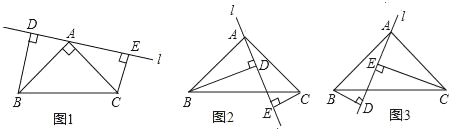
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BD⊥AE于D,CE⊥AE于E.求证:
(1)当直线l绕点A旋转到如图1位置时,试说明:DE=BD+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD﹣CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国传统数学最重要的著作,其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:有几个人共同出钱买鸡?鸡的价钱是多少?”设有x个人共同买鸡,根据题意列一元一次方程,正确的是( )

A. 9x﹣11=6x+16 B. 9x+11=6x﹣16 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
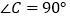 ,
,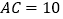 ,
,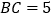 ,
,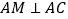 ,点
,点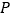 和点
和点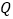 从
从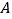 点出发,分别在射线
点出发,分别在射线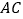 和射线
和射线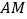 上运动,且
上运动,且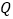 点运动的速度是
点运动的速度是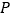 点运动的速度的
点运动的速度的 倍,当点
倍,当点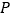 运动至__________时,
运动至__________时,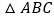 与
与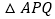 全等.
全等.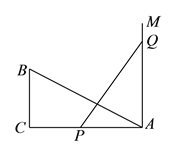
-
科目: 来源: 题型:
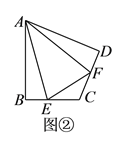
查看答案和解析>>【题目】(
 )如图①,在四边形
)如图①,在四边形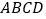 中,
中, ,
,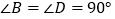 ,
,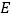 、
、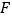 分别是边
分别是边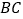 、
、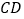 上的点,且
上的点,且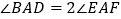 .
.求证:
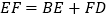 .
.(
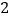 )如图②,在四边形
)如图②,在四边形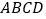 中,
中, ,
,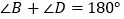 ,
,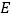 、
、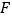 分别是边
分别是边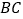 、
、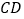 上的点,且
上的点,且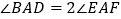 ,(
,(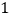 )中的结论是否仍然成立?
)中的结论是否仍然成立?(
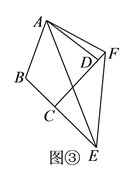
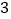 )如图③,在四边形
)如图③,在四边形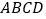 中,
中, ,
,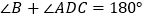 ,
,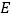 、
、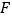 分别是边
分别是边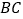 、
、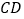 延长线上的点,且
延长线上的点,且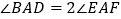 .(
.(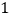 )中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.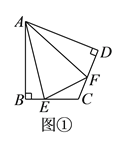
相关试题

