【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 将对角线
将对角线![]() 三等分,且
三等分,且![]() ,连接
,连接![]() .
.
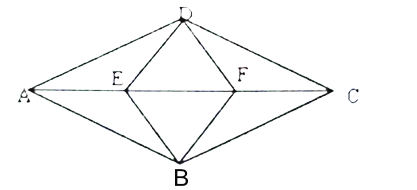
(1)求证:四边形![]() 为菱形
为菱形
(2)求菱形![]() 的面积;
的面积;
(3)若![]() 是菱形
是菱形![]() 的边上的点,则满足
的边上的点,则满足![]() 的点
的点![]() 的个数是______个.
的个数是______个.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)8
;(3)8
【解析】
(1)根据题意证明△AED≌△AEB≌△CFD≌△CFB,得到四边相等即可证明是菱形;
(2)求出菱形的对角线的长,利用菱形的面积等于对角线乘积的一半解决问题即可.
(3)不妨假设点P在线段AD上,作点E关于AD的对称点E′,连接FE′交AD于点P,此时PE+PF的值最小.求出PE+PF的最值,判断出在线段AD上存在两个点P满足条件,由此即可判断.
(1)∵四边形ABCD是菱形,
∴AD≡AB=CD=CB,∠DAE=∠BAE=∠DCF=∠BCF,
∴△AED≌△AEB≌△CFD≌△CFB(SAS)
∴DE=BE=DF=BF,
∴四边形DEBF为菱形.
(2)连接DB,交AC于O,

∵四边形ABCD是菱形,
∴DB⊥AC,![]() ,
,
又∵AE=EF=FC=2,
∴AO=3,AD=2DO,
∴![]() ,∴
,∴![]() ,
,
∴![]()
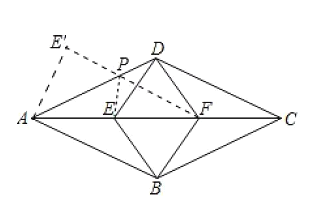
(3)不妨假设点P在线段AD上,作点E关于AD的对称点E′,连接FE′交AD于点P,此时PE+PF的值最小.
易知PE+PF的最小值=2![]()
当点P由A运动到D时,PE+PF的值由最大值6减小到2![]() 再增加到4,
再增加到4,
∵PE+PE=![]() ,2
,2![]() <
<![]() <4,
<4,
∴线段AD上存在两个点P,满足PE+PF=![]()
∴根据对称性可知:菱形ABCD的边上的存在8个点P满足条件.
故答案为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
 和点
和点 是线段
是线段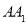 的两个端点,线段
的两个端点,线段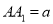 ,点
,点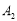 是点
是点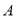 和点
和点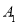 的对称中心,点
的对称中心,点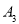 是点
是点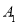 和点
和点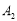 的对称中心,以此类推,(图中未画出)点
的对称中心,以此类推,(图中未画出)点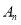 是点
是点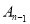 和点
和点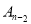 的对称中心.(
的对称中心.(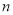 为正整数)
为正整数)
(1)填空:线段
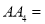 ____________ ;线段
____________ ;线段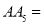 _____________ (用含
_____________ (用含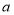 的最简代数式表示)
的最简代数式表示) (2)试写出线段
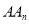 的长度(用含
的长度(用含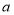 和
和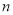 的代数式表示,无需说明理由)
的代数式表示,无需说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】某项工程由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍:若甲乙两队合作,则需12天完成,请问:
(1)甲,乙两队单独完成各需多少天;
(2)若施工方案是甲队先单独施工
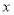 天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用
天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用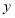 (万元)关于施工时间
(万元)关于施工时间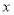 (天)的函数关系式
(天)的函数关系式(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
 给出以下结论:①当a=3时,方程组的解也是方程2x-y=a+13的解;②无论a取何值,x,y的值都不可能互为相反数;③x,y的自然数的解有2对;④若z=
给出以下结论:①当a=3时,方程组的解也是方程2x-y=a+13的解;②无论a取何值,x,y的值都不可能互为相反数;③x,y的自然数的解有2对;④若z= (x+3)y,则z的最大值是36.其中正确的是______.(填序号)
(x+3)y,则z的最大值是36.其中正确的是______.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】具备下列条件的三角形中,不是直角三角形的是( )
A. ∠A+∠B=∠C B. ∠B=∠C=
 ∠A
∠AC. ∠A=90°-∠B D. ∠A-∠B=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一面积为5
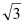 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)求x和y的值;
(2)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?
相关试题

