【题目】某项工程由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍:若甲乙两队合作,则需12天完成,请问:
(1)甲,乙两队单独完成各需多少天;
(2)若施工方案是甲队先单独施工![]() 天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用
天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用![]() (万元)关于施工时间
(万元)关于施工时间![]() (天)的函数关系式
(天)的函数关系式
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
参考答案:
【答案】(1)甲、乙两队单独完成分别需30天,20天;(2)y=0.5x+60;(3)甲队先施工10天,再甲乙合作8天,费用最低为55万元
【解析】
(1)设乙队单独完成需a天,则甲队单独完成需1.5a天,根据题意列出方程即可求解;
(2)设甲乙合作完成余下部分所需时间为w天,根据题意得到w与x的关系,根据题意即可写出y与x的关系式;
(3)根据施工期定为15~18天内完成得到x的取值范围,再根据一次函数的性质求出y的最小值.
(1)设乙队单独完成需a天,则甲队单独完成需1.5a天,
根据题意列:![]() ,
,
解得,a=20,经检验:a=20是所列方程的根,且符合题意,所以1.5a=30,
答:甲、乙两队单独完成分别需30天,20天;
(2)设甲乙合作完成余下部分所需时间为w天,
依题意得![]() ,
,
解得,w=![]() x+12
x+12
∴y=1.5x+(1.5+3.5)(![]() x+12)=-0.5x+60;
x+12)=-0.5x+60;
(3)由题可得15≤x![]() x+12≤18,
x+12≤18,
解得5≤x≤10,
∵y=-0.5x+60中k<0,
∴y随x的增大而减小,
∴当x=10时,y最小=-0.5×10+60=55,
此时,甲队先施工10天,再甲乙合作8天,费用最低为55万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分
人数/人
70
7
80
90
1
100
8
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
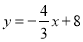 与
与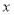 轴、
轴、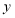 轴分别相交于点
轴分别相交于点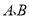 ,设
,设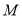 是线段
是线段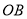 上一点,若将△
上一点,若将△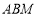 沿
沿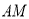 折叠,使点
折叠,使点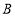 恰好落在
恰好落在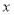 轴上的点
轴上的点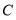 处。求:
处。求: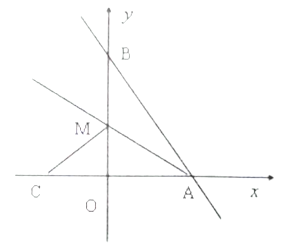
(1)点
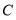 的坐标;
的坐标;(2)直线
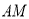 所对应的函数关系式.
所对应的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
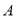 和点
和点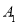 是线段
是线段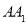 的两个端点,线段
的两个端点,线段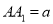 ,点
,点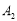 是点
是点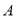 和点
和点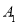 的对称中心,点
的对称中心,点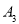 是点
是点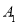 和点
和点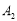 的对称中心,以此类推,(图中未画出)点
的对称中心,以此类推,(图中未画出)点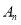 是点
是点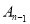 和点
和点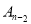 的对称中心.(
的对称中心.(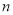 为正整数)
为正整数)
(1)填空:线段
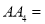 ____________ ;线段
____________ ;线段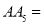 _____________ (用含
_____________ (用含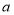 的最简代数式表示)
的最简代数式表示) (2)试写出线段
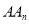 的长度(用含
的长度(用含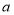 和
和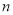 的代数式表示,无需说明理由)
的代数式表示,无需说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
 给出以下结论:①当a=3时,方程组的解也是方程2x-y=a+13的解;②无论a取何值,x,y的值都不可能互为相反数;③x,y的自然数的解有2对;④若z=
给出以下结论:①当a=3时,方程组的解也是方程2x-y=a+13的解;②无论a取何值,x,y的值都不可能互为相反数;③x,y的自然数的解有2对;④若z= (x+3)y,则z的最大值是36.其中正确的是______.(填序号)
(x+3)y,则z的最大值是36.其中正确的是______.(填序号) -
科目: 来源: 题型:
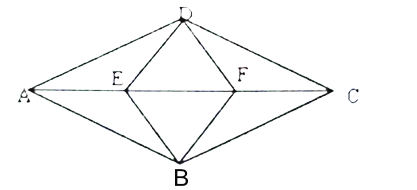
查看答案和解析>>【题目】如图,在菱形
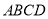 中,
中,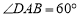 ,点
,点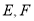 将对角线
将对角线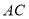 三等分,且
三等分,且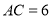 ,连接
,连接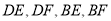 .
.
(1)求证:四边形
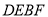 为菱形
为菱形(2)求菱形
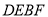 的面积;
的面积;(3)若
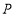 是菱形
是菱形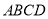 的边上的点,则满足
的边上的点,则满足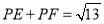 的点
的点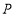 的个数是______个.
的个数是______个. -
科目: 来源: 题型:
查看答案和解析>>【题目】具备下列条件的三角形中,不是直角三角形的是( )
A. ∠A+∠B=∠C B. ∠B=∠C=
 ∠A
∠AC. ∠A=90°-∠B D. ∠A-∠B=90°
相关试题

