【题目】有一面积为5![]() 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
参考答案:
【答案】20![]() 或20.
或20.
【解析】
试题分析:分两种情形讨论①当30度角是等腰三角形的顶角,②当30度角是底角,
①当30度角是等腰三角形的顶角时,如图1中,
当∠A=30°,AB=AC时,设AB=AC=a,
作BD⊥AC于D,∵∠A=30°,
∴BD=![]() AB=
AB=![]() a,
a,
∴![]() a
a![]() a=5
a=5![]() ,
,
∴a2=20![]() ,
,
∴△ABC的腰长为边的正方形的面积为20![]() .
.
②当30度角是底角时,如图2中,
当∠ABC=30°,AB=AC时,作BD⊥CA交CA的延长线于D,设AB=AC=a,
∵AB=AC,
∴∠ABC=∠C=30°,
∴∠BAC=120°,∠BAD=60°,
在RT△ABD中,∵∠D=90°,∠BAD=60°,
∴BD=![]() a,
a,
∴![]() a
a![]() a=5
a=5![]() ,
,
∴a2=20,
∴△ABC的腰长为边的正方形的面积为20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在3月份举行读书节活动,鼓励学生进行有益的课外阅读,张老师为了了解该校学生课外阅读的情况,设计了“你最喜欢的课外读物类型”的调查问卷,包括“名著”“科幻”“历史”“童话”四类,在学校随机抽取了部分学生进行调查,被抽取的学生只能在四种类型中选择其中一类,最后将调查结果绘制成如下两幅尚不完整的统计图.
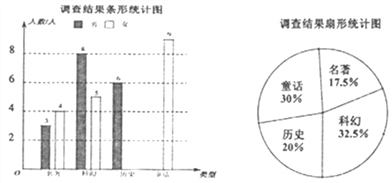
请你根据以上信息解答下列问题:
(1)本次调查中,张老师一共调查了 名学生;
(2)求本次调查中选择“历史”类的女生人数和“童话”类的男生人数,并将条形统计图补充完整;
(3)扇形图中“童话”类对应的圆心角度数为 .
(4)如果该校共有学生360名,请估算该校最喜欢“名著”类和“历史”类的学生总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体的六个面上分别标有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则a+b+c+abc=_____.
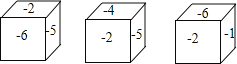
-
科目: 来源: 题型:
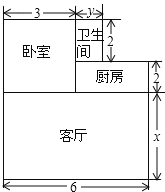
查看答案和解析>>【题目】小张准备购买一套新房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
(1)写出用含x、y的代数式表示的地面总面积;
(2)若x=5,y=1.5,铺设1m2地砖的平均费用为180元,则铺地砖的总费用为多少元?
-
科目: 来源: 题型:
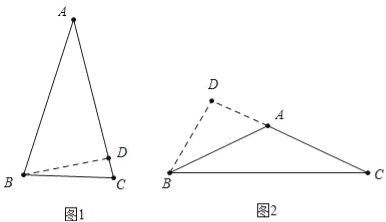
查看答案和解析>>【题目】(2016山东省菏泽市)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=
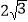 CM+
CM+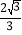 BN.
BN.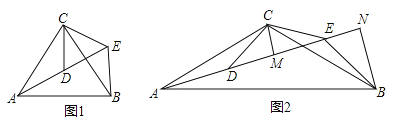
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC内接于
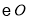 ,AB是直径,OD∥AC,AD=OC.
,AB是直径,OD∥AC,AD=OC.(1)求证:四边形OCAD是平行四边形;
(2)填空:①当∠B= 时,四边形OCAD是菱形;
②当∠B= 时,AD与
 相切.
相切.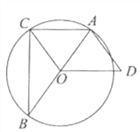
相关试题

