【题目】计算题
(1)解方程组:
① 
②![]()
(2)计算
①(π-2013)0-(![]() )-2+|-4|;
)-2+|-4|;
②4(a+2)(a+1)-7(a+3)(a-3)
(3)因式分解
①a4-16
②![]()
参考答案:
【答案】(1)①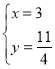 ;②
;②![]() ;(2)①-4;②
;(2)①-4;②![]() ;(3)①
;(3)①![]() ;②
;②![]() .
.
【解析】
(1)①方程组整理后,利用加减消元法求解即可;
②方程组利用加减消元法求解即可;
(2)①原式利用零指数幂、负整数指数幂法则,以及绝对值的代数意义化简,计算即可得到结果;
②原式利用多项式乘以多项式,以及平方差公式化简,去括号合并即可得到结果.
(3)①两次利用平方差公式因式分解即可;
②先提公因式﹣3x,然后利用完全平方公式因式分解即可.
(1)①方程组整理得:![]() ,
,
两式相加得:4x=12,即x=3,
把x=3代入x+4y=14得:y![]() ,
,
则方程组的解为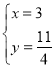 ;
;
②第一个式子×3+第二个式子×2,得:23x=46,即x=2,
把x=2代入5x-6y=4得:y=1,
则方程组的解为![]() ;
;
(2)①原式=1﹣9+4=﹣4;
②原式=4(a2+3a+2)﹣7(a2﹣9)
=4a2+12a+8﹣7a2+63
=﹣3a2+12a+71;
(3)①原式=![]()
=![]() ;
;
②原式=![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AE=ED=2,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把对角线相等的四边形叫做和美四边形.
 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子. 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形; 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O, ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
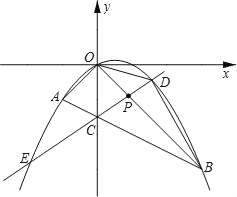
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).

(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.

试说明:AC∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中, ,中位线
,中位线 与对角线
与对角线 交于
交于 两点,若
两点,若 cm,
cm,  cm,则
cm,则 的长等于( )
的长等于( )
A. 10 cm B. 13 cm C. 20 cm D. 26 cm
相关试题

