搜索
【题目】如图，在梯形
中，
，中位线
与对角线
交于
两点，若
cm, 
cm，则
的长等于( )
A. 10 cm B. 13 cm C. 20 cm D. 26 cm
参考答案：
【答案】D
【解析】分析：根据梯形的中位线的定理和平行线分线段成比例定理求出AM=CM，NB=DN，然后根据三角形的中位线定理求出CD的长，然后再根据梯形的中位线定理求出AB的长即可.
详解：∵EF是梯形的中位线，
∴EF∥CD∥AB．
∴AM=CM，BN=DN．
∴EM是△ACD的中位线，NF是△BCD的中位线，
∴EM=
CD，NF=CD．
∴EM=NF=
=5，即CD=10．
∵EF是梯形ABCD的中位线，
∴DC+AB=2EF，即10+AB=2×18=36．
∴AB=26．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算题
（1）解方程组：
①
②
（2）计算
①(π-2013)0-(
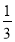)-2+|-4|；②4(a+2)(a+1)-7(a+3)(a-3)
（3）因式分解
①a4－16
②
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在等边三角形ABC中，BC＝8cm，射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t（s）．
（1）连接EF，当EF经过AC边的中点D时，求证：四边形AFCE是平行四边形；
（2）填空：①当t为 s时，四边形ACFE是菱形；②当t为 s时，△ACE的面积是△ACF的面积的2倍．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D．
试说明：AC∥DF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|.
利用数形结合思想回答下列问题：
①数轴上表示1和3两点之间的距离是
②数轴上表示x和-1的两点之间的距离表示为
③若x表示一个有理数，且-4<x<2，则|x-2|+|x+4|=
④若x表示一个有理数，且|x-2|+|x+4|=8，则有理数x的值是
-
科目： 来源： 题型：
查看答案和解析>>【题目】四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为
的小正方形EFGH，已知AM为Rt△ABM较长直角边，AM=
EF，则正方形ABCD的面积为（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】用A4纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元.在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为
（为非负整数）.（1）根据题意，填写下表：
一次复印页数（页）
5
10
20
30
…
甲复印店收费（元）
2
…
乙复印店收费（元）
…
（2）设在甲复印店复印收费
元，在乙复印店复印收费
元，分别写出
关于的函数关系式；（3）当
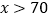时，顾客在哪家复印店复印花费少？请说明理由.
相关试题
