【题目】小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( ) 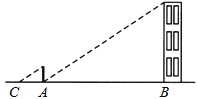
A.10米
B.12米
C.15米
D.22.5米
参考答案:
【答案】A
【解析】解答:∵ ![]() 即
即 ![]() ,
,
∴楼高=10米.
故选:A.
分析:在同一时刻物高和影长成正比,即在同一时刻的两个物体、影子、经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,列方程求解.此题考查了相似三角形在测量高度时的应用,解题的关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
【考点精析】掌握相似三角形的应用是解答本题的根本,需要知道测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
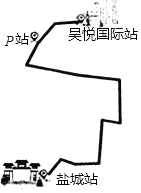
查看答案和解析>>【题目】常州每年举行一次“一袋牛奶的暴走”公益活动,用步行的方式募集善款,其中挑战型路线”的起点是淹城站,并沿着规定的线路到达终点吾悦国际站.甲、乙两组市民从起点同时出发,已知甲组的速度为6km/h,乙组的速度为5km/h,当甲组到达终点后,立即以3km/h的速度按原线路返回,并在途中的P站与乙组相遇,P站与吾悦国际站之间的路程为1.5km
(1)求“挑战型路线”的总长;
(2)当甲组到达终点时,乙组离终点还有多少路程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形ABCD对折,折痕为MN , 矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.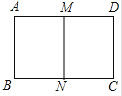
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC∽△ADE , AE:EC=5:3,BC=6cm,∠A=40°,∠C=45°.
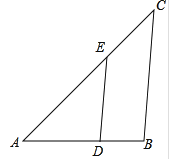
(1)求∠ADE的大小;
(2)求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
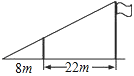
A.12m
B.10m
C.8m
D.7m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.
(1)求证:AC=BA.
(2)△ABC是什么三角形?请说明理由.
(3)如果AM⊥BC,那么AM=
 BC吗?请说明理由.
BC吗?请说明理由.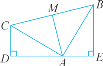
-
科目: 来源: 题型:
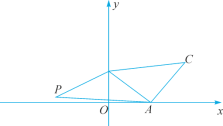
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(4,0),B(0,3),以线段AB为边在第一象限内作等腰直角三角形ABC,∠BAC=90°.若第二象限内有一点P
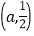 ,且△ABP的面积与△ABC的面积相等.
,且△ABP的面积与△ABC的面积相等.(1)求直线AB的函数表达式.
(2)求a的值.
(3)在x轴上是否存在一点M,使△MAC为等腰三角形?若存在,直接写出点M的坐标;若不存在,请说明理由.
相关试题

