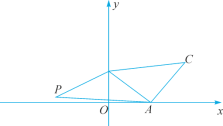
【题目】如图,在平面直角坐标系中,点A(4,0),B(0,3),以线段AB为边在第一象限内作等腰直角三角形ABC,∠BAC=90°.若第二象限内有一点P![]() ,且△ABP的面积与△ABC的面积相等.
,且△ABP的面积与△ABC的面积相等.
(1)求直线AB的函数表达式.
(2)求a的值.
(3)在x轴上是否存在一点M,使△MAC为等腰三角形?若存在,直接写出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=-![]() x+3;(2) a=-5;(3) 存在点M(-1,0)或(9,0)或(10,0)或(
x+3;(2) a=-5;(3) 存在点M(-1,0)或(9,0)或(10,0)或(![]() ,0),使△MAC为等腰三角形.
,0),使△MAC为等腰三角形.
【解析】设直线AB的函数表达式为y=kx+b(k≠0),把点A(4,0),B(0,3)代入,用待定系数法求解即可;
(2)利用勾股定理求出AB的长,从而求出△ABC的面积;过点P作PD⊥x轴于点D,根据S△ABP=S梯形PDOB+S△AOB-S△APD列式求解即可;
(3)分①当以点A为顶点时,②当以点C为顶点时,③当以点M为顶点时三种情况求解.
(1)设直线AB的函数表达式为y=kx+b(k≠0).由题意,得
![]() ,解得
,解得
∴直线AB的函数表达式为y=-![]() x+3.
x+3.
(2)如解图,过点P作PD⊥x轴于点D.

易得BO=3,AO=4,
∴AB=![]() =5.
=5.
∵△ABC是等腰直角三角形,AB=AC,
∴S△ABC=![]() .
.
∵点P(a,![]() )且在第二象限,
)且在第二象限,
∴PD=![]() ,OD=-a,
,OD=-a,
∴S△ABP=S梯形PDOB+S△AOB-S△APD
=![]() +
+![]() ×3×4-
×3×4-![]() ×(4-a)×
×(4-a)×![]() =-
=-![]() a+5,
a+5,
∴-![]() a+5=
a+5=![]() ,解得a=-5.
,解得a=-5.
(3)存在.
如解图,分三种情况讨论:
①当以点A为顶点时,以点A为圆心,AC长为半径画弧,交x轴于点M1,M2,
易知AM1=AM2=AC=5,
∴点M1(-1,0),M2(9,0).
②当以点C为顶点时,以点C为圆心,AC长为半径画弧,交x轴于点M3,过点C作CE⊥x轴于点E.
易知△AOB≌△CEA≌△CEM3,
∴EM3=AE=BO=3,CE=AO=4,
∴点M3(10,0).
③当以点M为顶点时,作AC的中垂线交x轴于点M4.
易得点C(7,4),
又∵点A(4,0),
∴AC的中点坐标为(![]() ,0).
,0).
易知AB平行于AC的中垂线,故可设AC中垂线的函数表达式为y=-![]() x+b.
x+b.
由题意,得-![]() ×
×![]() +b=2,解得b=
+b=2,解得b=![]() ,
,
∴AC中垂线的函数表达式为y=-![]() x+
x+![]() .
.
令y=0,得x=![]() ,
,
∴点M4(![]() ,0).
,0).
综上所述,存在点M(-1,0)或(9,0)或(10,0)或![]() ,使△MAC为等腰三角形.
,使△MAC为等腰三角形.
-
科目: 来源: 题型:
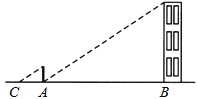
查看答案和解析>>【题目】小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米
B.12米
C.15米
D.22.5米 -
科目: 来源: 题型:
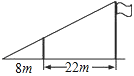
查看答案和解析>>【题目】如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
A.12m
B.10m
C.8m
D.7m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.
(1)求证:AC=BA.
(2)△ABC是什么三角形?请说明理由.
(3)如果AM⊥BC,那么AM=
 BC吗?请说明理由.
BC吗?请说明理由.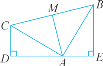
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知CA⊥BA
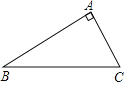
(1)画图:①延长BA到D,使AD=BA,连接CD;
②过点A画AE∥BC,AE与CD相交于点E;
③过点B画BF⊥CD,交DC的延长线于点F.
思考:图中有______条线段,它们的长度表示点到直线的距离;
(2)度量:
①你度量的哪些量?______;
②通过度量你发现:______.(写一条发现即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组的小明想测量教学楼前的一棵树的高度.下午课外活动时他测得一根长为1m的竹竿的影长是0.8m.但当他马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图).他先测得留在墙壁上的树影高为1.2m,又测得地面的影长为2.6m,请你帮他算一下,下列哪个数字最接近树高( )m.

A.3.04
B.4.45
C.4.75
D.3.8 -
科目: 来源: 题型:
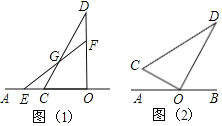
查看答案和解析>>【题目】如图,已知点O在直线AB上,将一副直角三角板的直角顶点放在点O处,其中∠OCD=60°,∠OEF=45°.边OC、OE在直线AB上.
(1)如图(1),若CD和EF相交于点G,则∠DGF的度数是______°;
(2)将图(1)中的三角板OCD绕点O顺时针旋转30°至图(2)位置
①若将三角板OEF绕点O顺时针旋转180°,在此过程中,当∠COE=∠EOD=∠DOF时,求∠AOE的度数;
②若将三角板OEF绕点O以每秒4°的速度顺时针旋转180°,与此同时,将三角板OCD绕点O以每秒1°的速度顺时针旋转,当三角板OEF旋转到终点位置时,三角板OCD也停止旋转.设旋转时间为t秒,当OD⊥EF时,求t的值.
相关试题

