搜索
【题目】如图，小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为（ ）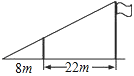 
A.12m
B.10m
C.8m
D.7m
参考答案：
【答案】A
【解析】解答：如图，∵ED⊥ADBC⊥AC∴ED∥BC
∴△AED∽△ABC
∴ 
而AD=8，AC=AD+CD=8+22=30，ED=3.2
∴BC= 
=12（m）
∴旗杆的高为12m．
故选：A．
分析：要求旗杆的高度BC ， 可证△AED∽△ABC ， 根据对应线段成比例，列出方程进行求解．此题考查了相似三角形在测量高度时的应用，解题的关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把矩形ABCD对折，折痕为MN ， 矩形DMNC与矩形ABCD相似，已知AB=4．
（1）求AD的长；
（2）求矩形DMNC与矩形ABCD的相似比．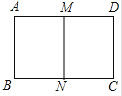
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，△ABC∽△ADE ， AE：EC=5：3，BC=6cm，∠A=40°，∠C=45°．
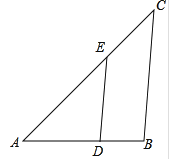
（1）求∠ADE的大小；
（2）求DE的长． -
科目： 来源： 题型：
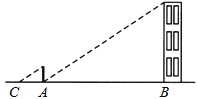
查看答案和解析>>【题目】小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（ ）
A.10米
B.12米
C.15米
D.22.5米 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠CDA＝∠AEB＝90°，且CD＝AE，AD＝BE.
(1)求证：AC＝BA.
(2)△ABC是什么三角形？请说明理由．
(3)如果AM⊥BC，那么AM＝
BC吗？请说明理由．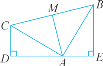
-
科目： 来源： 题型：
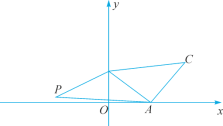
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A(4，0)，B(0，3)，以线段AB为边在第一象限内作等腰直角三角形ABC，∠BAC＝90°.若第二象限内有一点P
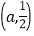，且△ABP的面积与△ABC的面积相等．(1)求直线AB的函数表达式．
(2)求a的值．
(3)在x轴上是否存在一点M，使△MAC为等腰三角形？若存在，直接写出点M的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知CA⊥BA
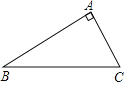
（1）画图：①延长BA到D，使AD=BA，连接CD；
②过点A画AE∥BC，AE与CD相交于点E；
③过点B画BF⊥CD，交DC的延长线于点F．
思考：图中有______条线段，它们的长度表示点到直线的距离；
（2）度量：
①你度量的哪些量？______；
②通过度量你发现：______．（写一条发现即可）
相关试题
