【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
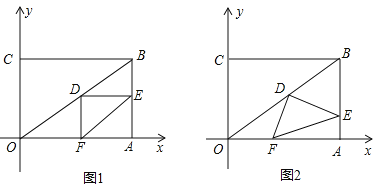
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
参考答案:
【答案】(1)3;(2)∠DEF的大小不变,tan∠DEF=![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题(1)当t=3时,点E为AB的中点,由三角形的中位线定理得出DE∥EA,DE=![]() OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
(2)作DM⊥OA于点M,DN⊥AB于N,证明四边形DMAN是矩形,得出∠MDN=90°,DM∥AB,DN∥OA,由平行线得出比例式![]() ,
,![]() ,由三角形中位线定理得出DM=
,由三角形中位线定理得出DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,证明ΔDMF∽ΔDNE,得出
OA=4,证明ΔDMF∽ΔDNE,得出![]() ,再由三角函数的定义即可得解;
,再由三角函数的定义即可得解;
(3)作DM⊥OA于M,DN⊥AB于N,若AD将ΔDEF的面积分为1:2的两部分,设AD交EF于点G,则点G为EF的三等分点.
①当点E到达中点之前时,NE=3-t,由ΔDMF∽ΔDNE得:MF=![]() ,求出AF=4+MF=
,求出AF=4+MF=![]() ,得出G(
,得出G(![]() ,
,![]() ),求出直线AD的解析式为y=-
),求出直线AD的解析式为y=-![]() +6,把G(
+6,把G(![]() ,
,![]() )代入即可求出t的值;
)代入即可求出t的值;
②当点超过中点之后,NE=t-3,由由ΔDMF∽ΔDNE得:MF=![]() ,求出AF=4-MF=
,求出AF=4-MF=![]() ,得出G(
,得出G(![]() ,
,![]() ),代入直线AD的解析式y=-
),代入直线AD的解析式y=-![]() +6即可求出t的值;
+6即可求出t的值;
试题解析: (1)当t=3时,点E为AB的中点,
∵A(8,0),C(0,6),
∴OA=8,OC=6,
∵点D为OB的中点,
∴DE∥OA,DE=![]() OA=4,
OA=4,
∵四边形OABC是矩形,
∴OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°,
∴四边形DFAE是矩形,
∴DF=AE=3;
(2)∠DEF的大小不变;理由如下:
作DM⊥OA于M,DN⊥AB于N,如图2所示:
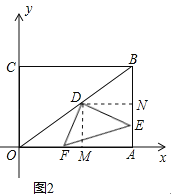
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM∥AB,DN∥OA,
∴![]() ,
,![]() ,
,
∵点D为OB的中点,
∴M、N分别是OA、AB的中点,
∴DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,
OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN,
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE,
∴![]() ,
,
∵∠EDF=90°,
∴tan∠DEF=![]() ;
;
(3)作DM⊥OA于M,DN⊥AB于N,
若AD将△DEF的面积分成1:2的两部分,
设AD交EF于点G,则点G为EF的三等分点;
①当点E到达中点之前时,如图3所示,NE=3﹣t,
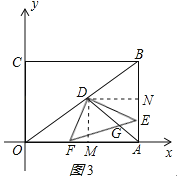
由△DMF∽△DNE得:MF=![]() (3﹣t),
(3﹣t),
∴AF=4+MF=﹣![]() t+
t+![]() ,
,
∵点G为EF的三等分点,
∴G(![]() ,
,![]() ),
),
设直线AD的解析式为y=kx+b,
把A(8,0),D(4,3)代入得:![]() ,
,
解得: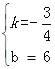 ,
,
∴直线AD的解析式为y=﹣![]() x+6,
x+6,
把G(![]() ,
,![]() )代入得:t=
)代入得:t=![]() ;
;
②当点E越过中点之后,如图4所示,NE=t﹣3,
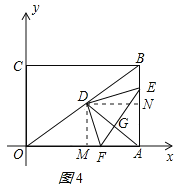
由△DMF∽△DNE得:MF=![]() (t﹣3),
(t﹣3),
∴AF=4﹣MF=﹣![]() t+
t+![]() ,
,
∵点G为EF的三等分点,
∴G(![]() ,
,![]() ),
),
代入直线AD的解析式y=﹣![]() x+6得:t=
x+6得:t=![]() ;
;
综上所述,当AD将△DEF分成的两部分的面积之比为1:2时,t的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是矩形
是矩形 两条对角线的交点,E是边
两条对角线的交点,E是边 上的点,沿
上的点,沿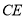 折叠后,点
折叠后,点 恰好与点
恰好与点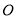 重合.若
重合.若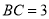 ,则折痕
,则折痕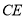 的长为 ( )
的长为 ( )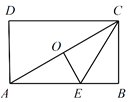
A.
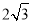 B.
B. 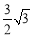 C.
C. 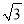 D. 6
D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设
 ,
, ,
, ,请探索
,请探索 ,
, ,
, 满足的等量关系。
满足的等量关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两人以相同路线前往距离单位10
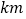 的培训中心参加学习.图中
的培训中心参加学习.图中 分别表示甲,乙两人前往目的地所走的路程s
分别表示甲,乙两人前往目的地所走的路程s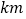 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8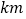 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )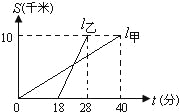
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式
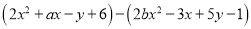
(1)若多项式的值与字母
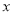 的取值无关,求
的取值无关,求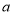 ,
,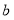 的值;
的值;(2)在(1)的条件下,先化简多项式
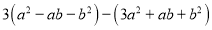 ,再求它的值;
,再求它的值;(3)在(1)的条件下,求
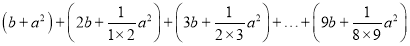 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:数轴上有
 、
、 两点,分别对应的数为
两点,分别对应的数为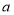 ,
,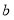 ,已知
,已知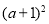 与
与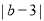 互为相反数,点
互为相反数,点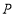 为数轴上一动点,对应为
为数轴上一动点,对应为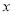 .
.(1)若点
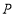 到点
到点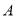 和点
和点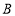 的距离相等,求点
的距离相等,求点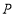 对应的数;
对应的数;(2)数轴上是否存在点
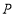 ,使点
,使点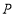 到点
到点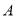 和点
和点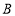 的距离之和为5?若存在,请求出
的距离之和为5?若存在,请求出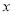 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;(3)当点
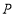 以每分钟1个单位长度的速度从
以每分钟1个单位长度的速度从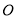 点向左运动,点
点向左运动,点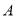 以每分钟5个单位长度向左运动,点
以每分钟5个单位长度向左运动,点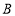 以每分钟20个单位长度的速度向左运动,问几分钟时点
以每分钟20个单位长度的速度向左运动,问几分钟时点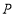 到点
到点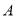 、点
、点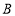 的距离相等.
的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据a、b、c、d. e方差为3,则另一组数据a+3,b+3,c+3,d+3,e+3的方差为___ ,
相关试题

