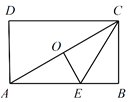
【题目】如图,点![]() 是矩形
是矩形![]() 两条对角线的交点,E是边
两条对角线的交点,E是边![]() 上的点,沿
上的点,沿![]() 折叠后,点
折叠后,点![]() 恰好与点
恰好与点![]() 重合.若
重合.若![]() ,则折痕
,则折痕![]() 的长为 ( )
的长为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
参考答案:
【答案】A
【解析】
由矩形的性质可得OA=OC,根据折叠的性质可得OC=BC,∠COE=∠B=90°,即可得出BC=![]() AC,OE是AC的垂直平分线,可得∠BAC=30°,根据垂直平分线的性质可得CE=AE,根据等腰三角形的性质可得∠OCE=∠BAC=30°,在Rt△OCE中利用含30°角的直角三角形的性质即可求出CE的长.
AC,OE是AC的垂直平分线,可得∠BAC=30°,根据垂直平分线的性质可得CE=AE,根据等腰三角形的性质可得∠OCE=∠BAC=30°,在Rt△OCE中利用含30°角的直角三角形的性质即可求出CE的长.
∵点O是矩形ABCD两条对角线的交点,
∴OA=OC,
∵沿CE折叠后,点B恰好与点O重合.BC=3,
∴OC=BC=3,∠COE=∠B=90°,
∴AC=2BC=6,OE是AC的垂直平分线,
∴AE=CE,
∵∠B=90°,BC=![]() AC,
AC,
∴∠BAC=30°,
∴∠OCE=∠BAC=30°,
∴OC=![]() CE,
CE,
∴CE=2![]() .
.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 中位数就是一组数据中最中间的一个数
B.
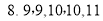 这组数据的众数是9
这组数据的众数是9C. 如果
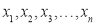 的平均数是1,那么
的平均数是1,那么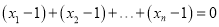
D. 一组数据的方差是这组数据的极差的平方
-
科目: 来源: 题型:
查看答案和解析>>【题目】某楼盘一楼是车库(暂不销售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
【1】
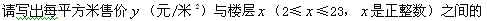 函数解析式;
函数解析式;【2】小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
【3】有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体的数据阐明你的看法。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+
x+ 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点D是劣弧AO上一动点(D点与A,C不重合).抛物线y=-
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点D是劣弧AO上一动点(D点与A,C不重合).抛物线y=- x+bx+c经过点A、C,与x轴交于另一点B,
x+bx+c经过点A、C,与x轴交于另一点B,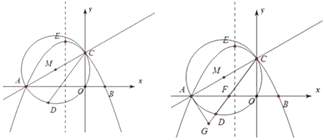
(1)求抛物线的解析式及点B的坐标;
(2)在抛物线的对称轴上是否存在一点P,是︱PA—PC︱的值最大;若存在,求出点P的坐标;若不存在,请说明理由。
(3)连CD交AO于点F,延长CD至G,使FG=2,试探究当点D运动到何处时,直线GA与⊙M相切,并请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设
 ,
, ,
, ,请探索
,请探索 ,
, ,
, 满足的等量关系。
满足的等量关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两人以相同路线前往距离单位10
 的培训中心参加学习.图中
的培训中心参加学习.图中 分别表示甲,乙两人前往目的地所走的路程s
分别表示甲,乙两人前往目的地所走的路程s 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )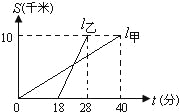
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
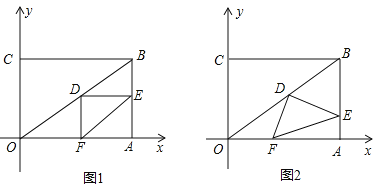
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
相关试题

