【题目】某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元
(1)若该超市一次性购进两种商品共80件,且恰好用去1 600元,则购进甲商品件,乙商品件;
(2)若该超市要使两种商品共80件的购进费用不超过1 640元,且总利润(利润=售价-进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
参考答案:
【答案】
(1)40;40
(2)解:(1)设该超市购进甲商品x件 ,则购进乙商品(80-x)件,由题意得 :
10x+30(80-x)=1600 ,
解得 x=40 ,
∴ 购进乙商品的数量为 :80-40=40件。
答 ;超市购进甲商品40件,购进乙商品40件 。
(2)设该超市购进甲商品a件,则购进乙商品(80-a)件,
由题意得 ![]()
解得38≤a≤40,因为a为正整数,
所以a=38,39,40.相应地,80-a=42,41,40.
进而利润分别为
(15-10)×38+(40-30)×42=190+420=610(元),(15-10)×39+(40-30)×41=195+410=605(元),(15-10)×40+(40-30)×40=200+400=600(元),则使该超市利润最大的方案是购进甲商品38件,乙商品42件.
【解析】(1)设该超市购进甲商品x件 ,则购进乙商品(80-x)件,根据购进甲商品的费用+购进乙商品的费用=1600,列出方程,求解即可;
(2)设该超市购进甲商品a件,则购进乙商品(80-a)件,根据购进甲商品的费用+购进乙商品的费用不超过1 640,售完甲商品的利润+售完乙商品的利润不少于600元.列出不等式组,求解得出a的取值范围,根据a为正整数,从而得出a的值为38,39,40.相应地,80-a=42,41,40.然后分别计算出每种进货方案的利润,再比较总利润即可得出最佳进货方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 轴于点
轴于点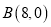 ,
,  ,反比例函数
,反比例函数 与OA、AB分别相交于点D、C,且点D为OA的中点,
与OA、AB分别相交于点D、C,且点D为OA的中点,(1)求反比例函数的解析式
(2)过点B的直线
 与反比例函数
与反比例函数 图象交于第三象限内一点F,求四边形
图象交于第三象限内一点F,求四边形 的面积
的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1 520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)每本文学名著元,每本动漫书元;
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总本数不低于72本,总费用不超过2 000元,请求出所有符合条件的购书方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在矩形ABCD中,点P为边BC上一点,且
 ,
,  ,求BP的长;
,求BP的长;(2)如图2,在平行四边形ABCD中,
 ,求
,求 的长;
的长;
(3)如图3,在四边形ABCD中,AD∥BC,
 ,
,  ,在BC边上存在一点P,使得
,在BC边上存在一点P,使得 ,则边
,则边 的长满足的条件为 。(请直接写出结果)
的长满足的条件为 。(请直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解正确的是( )
A.x2+xy+x=x(x+y)B.x2﹣4x+4=(x+2)(x﹣2)
C.a2﹣2a+2=(a﹣1)2+1D.x2﹣6x+5=(x﹣5)(x﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形腰长为6cm,一腰上的中线将其周长分成两部分,且两部分的差为3cm,则底边长为______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒

当t = 4时,求线段PQ的长度
(2)当t为何值时,△PCQ是等腰三角形?
(3)当t为何值时,△PCQ的面积等于16cm2?
(4)当t为何值时,△PCQ∽△ACB
相关试题

