【题目】(1)如图1,在矩形ABCD中,点P为边BC上一点,且![]() ,
, ![]() ,求BP的长;
,求BP的长;
(2)如图2,在平行四边形ABCD中, ![]() ,求
,求![]() 的长;
的长;

(3)如图3,在四边形ABCD中,AD∥BC, ![]() ,
, ![]() ,在BC边上存在一点P,使得
,在BC边上存在一点P,使得![]() ,则边
,则边![]() 的长满足的条件为 。(请直接写出结果)
的长满足的条件为 。(请直接写出结果)

参考答案:
【答案】(1)2;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由四边形ABCD是矩形,得到∠B=∠C=90°,根据余角的性质得到∠BAP=∠DPC,推出△ABP∽△PCD,根据相似三角形的性质即可得到结论;
(2)延长BC至点E,使得CD⊥DE,通过△ABP∽△DPE,列方程得到BP=1,过点P作PF⊥AB,解直角三角形即可得到结论;
(3)作AE⊥BC,DF⊥BC,得到∠AEP=∠DFP=90°,推出△AEP∽△PFD,根据相似三角形的性质得到AEDF=PEPF=4,由PE+PF≥2 ![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵∠APD=∠B=90°,
∴∠PAB+∠APB=∠APB+∠DPC=90°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴![]() ,
,
设BP=x,∴![]()
∴x1=2,x2=8,又BP<PC,
∴BP=2;
(2)延长BC至点E,使得CD⊥DE,
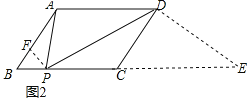
∵AB=2![]() ,BC=5,∠APD=∠B=45°,
,BC=5,∠APD=∠B=45°,
∴∠DPE=∠BAP,∠B=∠E=45°,
∴△ABP∽△DEP,
∴![]() ,
,
设BP=x,CE=![]() CD=4,
CD=4,
∴![]() ,
,
∴BP=1,
过点P作PF⊥AB,
则BF=PF=![]() ,AF=
,AF=![]() ,
,
∴AP=![]() ;
;
(3)AD≥4,
作AE⊥BC,DF⊥BC,
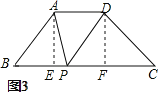
∴∠AEP=∠DFP=90°,
∵∠APD=90°,
∴∠EAP+∠APE=∠APE+∠DPF=90°,
∴∠EAP=∠DPF,
∴△AEP∽△PFD,
∴![]() ,
,
∴AEDF=PEPF=4,
∵PE+PF≥2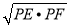 ,
,
∴AD=PE+PF≥4.
故答案为:AD≥4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣4的绝对值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 轴于点
轴于点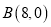 ,
,  ,反比例函数
,反比例函数 与OA、AB分别相交于点D、C,且点D为OA的中点,
与OA、AB分别相交于点D、C,且点D为OA的中点,(1)求反比例函数的解析式
(2)过点B的直线
 与反比例函数
与反比例函数 图象交于第三象限内一点F,求四边形
图象交于第三象限内一点F,求四边形 的面积
的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1 520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)每本文学名著元,每本动漫书元;
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总本数不低于72本,总费用不超过2 000元,请求出所有符合条件的购书方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元
(1)若该超市一次性购进两种商品共80件,且恰好用去1 600元,则购进甲商品件,乙商品件;
(2)若该超市要使两种商品共80件的购进费用不超过1 640元,且总利润(利润=售价-进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解正确的是( )
A.x2+xy+x=x(x+y)B.x2﹣4x+4=(x+2)(x﹣2)
C.a2﹣2a+2=(a﹣1)2+1D.x2﹣6x+5=(x﹣5)(x﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形腰长为6cm,一腰上的中线将其周长分成两部分,且两部分的差为3cm,则底边长为______cm.
相关试题

