【题目】等腰三角形的一个内角是50度,它的一腰上的高与底边的夹角是( )度.
A.25
B.40
C.25或40
D.60
参考答案:
【答案】C
【解析】解:当顶角为50°时,底角为(180°﹣50°)÷2=65°.
此时它的一条腰上的高与底边的夹角为90°﹣65°=25°.
当底角为50°时,此时它的一条腰上的高与底边的夹角为90°﹣50°=40°
故选C.
【考点精析】通过灵活运用等腰三角形的性质,掌握等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下图的方式搭图形:

(1)图① 根火柴棒;图②有 根火柴棒;图③有 根火柴棒.
(2)按上面的方法继续下去,第100个图形中有多少根火柴棒?
(3)第n(n≥1的整数)个图形中有多少根火柴棒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面去截一个长方体,截面的形状不可能是( )
A. 四边形 B. 五边形 C. 六边形 D. 七边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到 “分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数
 满足
满足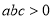 ,求
,求 的值.
的值.【解决问题】
解:由题意,得
 三个有理数都为正数或其中一个为正数,另两个为负数.
三个有理数都为正数或其中一个为正数,另两个为负数.①
 都是正数,即
都是正数,即 时,则
时,则 ;
;②当
 中有一个为正数,另两个为负数时,不妨设
中有一个为正数,另两个为负数时,不妨设 ,则
,则 .
.综上所述,
 值为3或-1.
值为3或-1.【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数
 满足
满足 ,求
,求 的值;
的值;(2)若
 为三个不为0的有理数,且
为三个不为0的有理数,且 ,求
,求 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是由一些火柴棒搭成的图案:

(1)摆第①个图案用______根火柴棒,摆第②个图案用______根火柴棒,摆第③个图案用______根火柴棒;
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.
求证:BF=AE.

(2) 如图2,正方形ABCD边长为12,将正方形沿MN折叠,使点A落在DC边上的点E处,且DE=5,求折痕MN的长。

(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,
∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,则 GH=___________;
②如图4,矩形ABCD由n个全等的正方形组成,则 GH=___________;(用n的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个角是110°,则它的底角是_____.
相关试题

