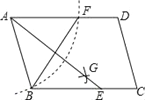
【题目】如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为____.
参考答案:
【答案】8
【解析】
由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=![]() BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
解:连结EF,AE与BF交于点O,如图,
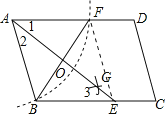
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=![]() BF=3,
BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=![]() =4,
=4,
∴AE=2AO=8.
故答案为:8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育彩票经销商计划用4500元从省体彩中心购进彩票20捆,已知体彩中心有
 、
、 、
、 三种不同价格的彩票,进价分别是
三种不同价格的彩票,进价分别是 彩票每捆150元,
彩票每捆150元, 彩票每捆200元,
彩票每捆200元, 彩票每捆250元.
彩票每捆250元.(1)若经销商同时购进两种不同型号的彩票20捆,刚好用去4500元,请你帮助设计进票方案;
(2)若销售
 型彩票每捆获手续费20元,
型彩票每捆获手续费20元, 型彩票每捆获手续费30元,
型彩票每捆获手续费30元, 型彩票每捆获手续费50元.在问题(1)设计的购进两种彩票的方案中,为使销售完时获得的手续费最多,你选择哪种进票方案?
型彩票每捆获手续费50元.在问题(1)设计的购进两种彩票的方案中,为使销售完时获得的手续费最多,你选择哪种进票方案?(3)若经销商准备用4500元同时购进
 、
、 、
、 三种彩票20捆,请你帮助经销商设计进票方案.
三种彩票20捆,请你帮助经销商设计进票方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.

(1)求证:∠BDC=∠A;
(2)若CE=2,DE=1,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图把
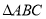 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到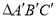 .
.(1)在图中画出
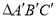 ;
;(2)写出点
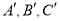 的坐标:
的坐标: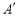 的坐标为______,
的坐标为______,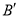 的坐标为 _________;
的坐标为 _________; 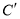 的坐标为________.
的坐标为________.(3)在
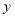 轴上是否存在一点P,使得
轴上是否存在一点P,使得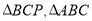 的面积相等?若存在,请求出点P的坐标;若不存在,说明理由.
的面积相等?若存在,请求出点P的坐标;若不存在,说明理由.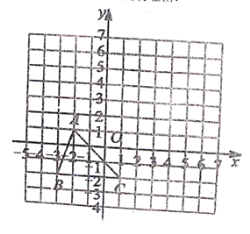
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,垂足分别为D,F,试说明:
,垂足分别为D,F,试说明: 请补充说明过程,并在括号内填上理由
请补充说明过程,并在括号内填上理由解:
 (已知)
(已知)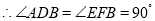 ( )
( ) ( )
( ) ( )
( ) (已知)
(已知) ( )
( ) ( )
( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 .
.


(1)如图1,直接写出
 ,
, 和
和 之间的数量关系.
之间的数量关系.(2)如图2,
 ,
, 分别平分
分别平分 ,
, ,那么
,那么 和
和 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.(3)若点E的位置如图3所示,
 ,
, 仍分别平分
仍分别平分 ,
, ,请直接写出
,请直接写出 和
和 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】大于
 的正整数
的正整数 的三次幂可“裂变”成若干个连续奇数的和,如
的三次幂可“裂变”成若干个连续奇数的和,如 ,
, ,
, ,
, .若
.若 “裂变”后,其中有一个奇数是
“裂变”后,其中有一个奇数是 ,则
,则 的值是( )
的值是( )A.
 B.
B. C.
C.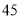 D.
D.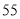
相关试题

