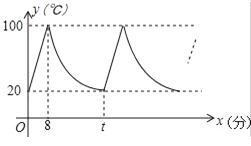
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?
参考答案:
【答案】(1)y=10x+20;(2)t=40;(3)小明散步45分钟回到家时,饮水机内的温度约为70℃.
【解析】(1)由函数图象可设函数解析式,再由图中坐标代入解析式,即可求得y与x的关系式;
(2)首先求出反比例函数解析式进而得到t的值;
(3)利用已知由x=5代入求出饮水机的温度即可.
(1)当0≤x≤8时,设水温y(℃)与开机时间x(分)的函数关系为:y=kx+b,
依据题意,得![]() ,解得:
,解得:![]() ,
,
故此函数解析式为:y=10x+20;
(2)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为:y=![]() ,
,
依据题意,得:100=![]() ,即m=800,故y=
,即m=800,故y=![]() ,
,
当y=20时,20=![]() ,解得:t=40;
,解得:t=40;
(3)∵45﹣40=5≤8,
∴当x=5时,y=10×5+20=70,
答:小明散步45分钟回到家时,饮水机内的温度约为70℃.
“点睛”本题主要考查了一次函数及反比例函数的应用题,根据题意得出正确的函数解析式是解题关键,同学们在解答时要读懂题意,才不易出错.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的有( )
①相等的角是对顶角; ②在同一平面内,若a∥b,b∥c,则a∥c;
③同旁内角互补; ④互为邻补角的两角的角平分线互相垂直.
A.4个B.1个C.2个D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上,AH=2.
(1)如图1,当DG=2,且点F在边BC上时.
求证:① △AHE≌△DGH;
② 菱形EFGH是正方形;
(2)如图2,当点F在正方形ABCD的外部时,连接CF.
① 探究:点F到直线CD的距离是否发生变化?并说明理由;
② 设DG=x,△FCG的面积为S,是否存在x的值,使得S=1,若存在,求出x的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=
 AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.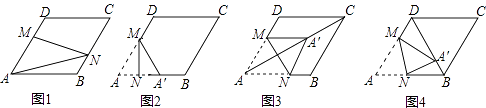
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.

(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=
 AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE. 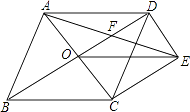
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )
A.(﹣2,﹣3)
B.(﹣2,3)
C.(2,﹣3)
D.(2,3)
相关试题

