【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM= ![]() AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.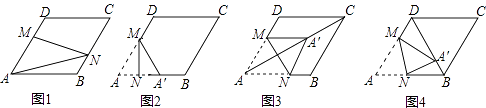
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)![]()
(2)1,解:②在菱形ABCD中,AC平分∠DAB,∵∠DAB=60°,∴∠DAC=∠CAB=30°,∵△AMN沿MN翻折得到△A′MN,∴AC⊥MN,AM=A′M,AN=A′N,;∴∠AMN=∠ANM=60°,∴AM=AN,∴AM=A′M=AN=A′N,∴四边形AM A′N是菱形;,③在菱形ABCD中,AB=AD,∴∠ADB=∠ABD=60°,∴∠BA′M=∠DMA′+∠ADB,∴A′M=AM=2,∠NA′M=∠A=60°,∴∠NA′B=∠DMA′,∴△DMA′∽△BA′N,∴ ![]() =
= ![]() ,∵MD=
,∵MD= ![]() AD=1,A′M=2,∴
AD=1,A′M=2,∴ ![]() =
= ![]()
【解析】解:(1)如图1,
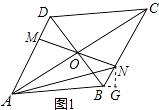
过点N作NG⊥AB于G,
∵四边形ABCD是菱形,
∴AD∥BC,OD=OB,
∴ ![]() =
= ![]() =1,
=1,
∴BN=DM= ![]() AD=1,
AD=1,
∵∠DAB=60°,
∴∠NBG=60°
∴BG= ![]() ,GN=
,GN= ![]() ,
,
∴AN= ![]() =
= ![]() =
= ![]() ;
;
故答案为: ![]() ;
;
( 2 )①当点A′落在AB边上,则MN为AA′的中垂线,
∵∠DAB=60°AM=2,
∴AN= ![]() AM=1,
AM=1,
故答案为:1;
(1)过点N作NG⊥AB于G,构造直角三角形,根据菱形的性质得出AD∥BC,OD=OB,∠NBG=60° ,根据平行线分线段成比例定理得出DM∶BN=OD∶OB=1,从而得出BN=DM=1 ,利用含30°的直角三角形的边的关系得出BG、GN的长,利用勾股定理解决问题;
(2)①利用线段中垂线的性质得到MN⊥AA',利用含30°的直角三角形的边的关系得出AN的长;
②利用菱形的性质得到对角线平分每一组对角,得到∠DAC=∠CAB=30°,根据翻折的性质得到AC⊥MN,AM=A′M,AN=A′N,∠AMN=∠ANM=60°,AM=AN,AM=A′M=AN=A′N,四边形AM A′N是菱形
③根据菱形的性质得到AB=AD,∠ADB=∠ABD=60°,求得∠NA′M=∠DMA′+∠ADB,证得A′M=AM=2,∠NA′M=∠A=60°,得到∠NA′B=∠DMA′,从而判断出△DMA′∽△BA′N,利用相似三角形对应边成比例得到结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A.版画 B.保龄球C.航模 D.园艺种植,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的保龄球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加保龄球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的有( )
①相等的角是对顶角; ②在同一平面内,若a∥b,b∥c,则a∥c;
③同旁内角互补; ④互为邻补角的两角的角平分线互相垂直.
A.4个B.1个C.2个D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上,AH=2.
(1)如图1,当DG=2,且点F在边BC上时.
求证:① △AHE≌△DGH;
② 菱形EFGH是正方形;
(2)如图2,当点F在正方形ABCD的外部时,连接CF.
① 探究:点F到直线CD的距离是否发生变化?并说明理由;
② 设DG=x,△FCG的面积为S,是否存在x的值,使得S=1,若存在,求出x的值;若不存在,请说明理由. -
科目: 来源: 题型:
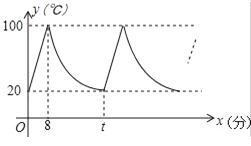
查看答案和解析>>【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.

(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=
 AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE. 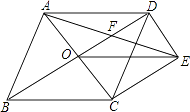
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
相关试题

