【题目】某小区为了美化环境,计划分两次购进A,B两种花,第一次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.
(1)求A、B两种花的单价分别是多少元?
(2)若购买A、B两种花共31棵,且B种花的数量不多于A种花的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
参考答案:
【答案】(1)A种花的单价为20元,B种花的单价为5元.(2)购进A种花11棵、B种花20棵时,费用最省,最省费用是320元.
【解析】分析:(1)设A种花草每棵的价格x元,B种花草每棵的价格y元,根据第一次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.列出方程组,即可解答.
(2)设A种花草的数量为m棵,则B种花草的数量为(31m)棵,根据B种花草的数量不多于A种花草的数量的2倍,得出m的范围,设总费用为W元,根据总费用=两种花草的费用之和建立函数关系式,由一次函数的性质就可以求出结论.
详解:(1)设A种花草每棵的价格x元,B种花草每棵的价格y元,根据题意得:![]()
解得:![]()
∴A种花草每棵的价格是20元,B种花草每棵的价格是5元。
(2)设A种花草的数量为m棵,则B种花草的数量为(31m)棵,
∵B种花草的数量不多于A种花草的数量的2倍,
∴![]()
解得:![]()
∵m是正整数,
∴m最小值=11,
设购买树苗总费用为W=20m+5(31m)=15m+155,
∵k>0,
∴W随x的减小而减小,
当m=11时,W最小值=15×11+155=320(元).
答:购进A种花草的数量为11棵、B种20棵,费用最省;最省费用是320元.
点睛:考查一次函数的应用, 二元一次方程组的应用,关键是找出题目中的等量关系列出方程组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD两邻边的长m,n是关于x的方程
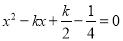 的两个实数根.
的两个实数根.(1)求k的取值范围.
(2)当k为何值时,四边形ABCD的两条对角线的长相等,且都等于
 ,求出这时四边形ABCD的周长和面积.
,求出这时四边形ABCD的周长和面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a,b,其中B,C,E在一条直线上,G在线段CD上,三角形AGE的面积为S.
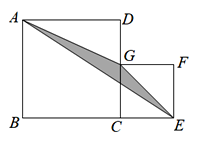
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a,b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
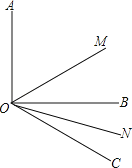
(1)求∠MON的度数;
(2)如果∠AOB=α,其他条件不变,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣
 ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积在数量上相等,则这个点叫做和谐点.
(1)判断点M(﹣1,2),N(﹣4,﹣4)是否为和谐点,并说明理由;
(2)若和谐点P(a,3)在直线y=﹣x+b(b为常数)上,试求a,b的值.
相关试题

